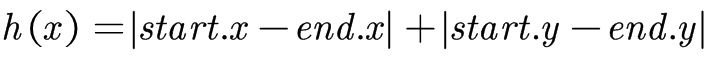最近开始接触寻路算法,对此不太了解的话建议读者先看这篇文章《如何快速找到最优路线?深入理解游戏中寻路算法》 。
所有寻路算法都需要一种方法以数学的方式估算某个节点是否应该被选择。大多数游戏都会使用启发式 (heuristic) ,以 h(x) 表示,就是估算从某个位置到目标位置的开销。理想情况下,启发式结果越接近真实越好。
——《游戏编程算法与技巧》
今天主要说的是贪婪最佳优先搜索(Greedy Best-First Search),贪心算法的含义是:求解问题时,总是做出在当前来说最好的选择。通俗点说就是,这是一个“短视”的算法。
为什么说是“短视”呢?首先要明白一个概念:曼哈顿距离 。
曼哈顿距离
曼哈顿距离被认为不能沿着对角线移动,如下图中,红、蓝、黄线都代表等距离的曼哈顿距离。绿线代表欧氏距离 ,如果地图允许对角线移动的话,曼哈顿距离会经常比欧式距离高。
在 2D 地图中,曼哈顿距离的计算如下:
贪婪最佳优先搜索的简介
贪婪最佳优先搜索的每一步,都会查找相邻的节点,计算它们距离终点的曼哈顿距离,即最低开销的启发式。
贪婪最佳优先搜索在障碍物少的时候足够的快,但最佳优先搜索得到的都是次优的路径。例如下图,算法不断地寻找当前 h(启发式)最小的值,但这条路径很明显不是最优的。
贪婪最佳优先搜索“未能远谋”,大多数游戏都要比贪婪最佳优先算法所能提供的更好的寻路,但大多数寻路算法都是基于贪婪算法,所以了解该算法很有必要。
首先是节点类,每个节点需要存储上一个节点的引用和 h 值,其他信息是为了方便算法的实现。存储上一个节点的引用是为了像一个链表一样,最后能通过引用得到路径中所有的节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public class Node { public Node parent; public float h; public List<Node> adjecent = new List<Node>(); public int row; public int col; public void Clear () { parent = null ; h = 0.0f ; } }
下面是图类,图类最主要的任务就是根据提供的二维数组初始化所有的节点,包括寻找他们的相邻节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 public class Graph { public int rows = 0 ; public int cols = 0 ; public Node[] nodes; public Graph (int [, ] grid { rows = grid.GetLength(0 ); cols = grid.GetLength(1 ); nodes = new Node[grid.Length]; for (int i = 0 ; i < nodes.Length; i++) { Node node = new Node(); node.row = i / cols; node.col = i - (node.row * cols); nodes[i] = node; } foreach (Node node in nodes) { int row = node.row; int col = node.col; if (grid[row, col] != 1 ) { if (row > 0 && grid[row - 1 , col] != 1 ) { node.adjecent.Add(nodes[cols * (row - 1 ) + col]); } if (col < cols - 1 && grid[row, col + 1 ] != 1 ) { node.adjecent.Add(nodes[cols * row + col + 1 ]); } if (row < rows - 1 && grid[row + 1 , col] != 1 ) { node.adjecent.Add(nodes[cols * (row + 1 ) + col]); } if (col > 0 && grid[row, col - 1 ] != 1 ) { node.adjecent.Add(nodes[cols * row + col - 1 ]); } } } } }
在算法类中,我们需要记录开放集合和封闭集合。开放集合指的是当前步骤我们需要考虑的节点,例如算法开始时就要考虑初始节点的相邻节点,并从其找到最低的 h(x) 值开销的节点。封闭集合存放已经计算过的节点。
1 2 3 4 public List<Node> reachable;public List<Node> explored;
下面是算法主要的逻辑,额外的函数可以查看项目源码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 public Stack<Node> Finding (){ Stack<Node> path; Node currentNode = reachable[0 ]; while (currentNode != destination) { explored.Add(currentNode); reachable.Remove(currentNode); AddAjacent(currentNode); if (reachable.Count == 0 ) { return null ; } currentNode = FindLowestH(); } path = new Stack<Node>(); Node node = destination; path.Push(node); while (node.parent != null ) { path.Push(node.parent); node = node.parent; } return path; }
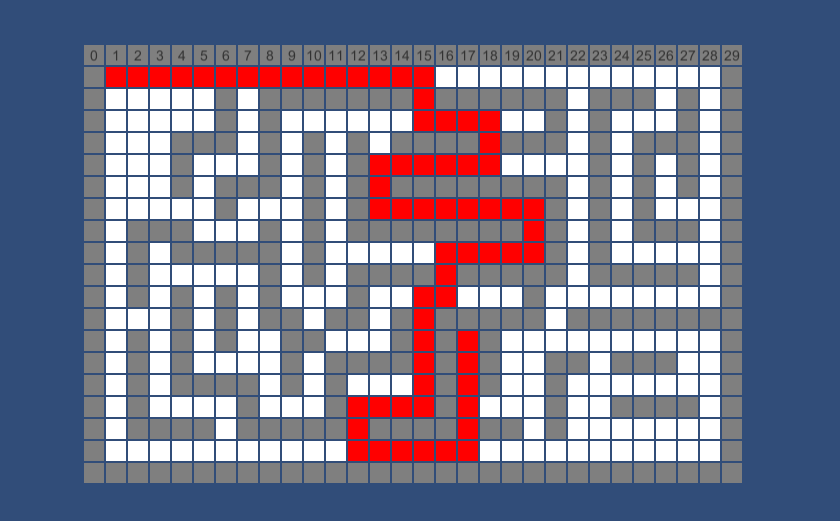
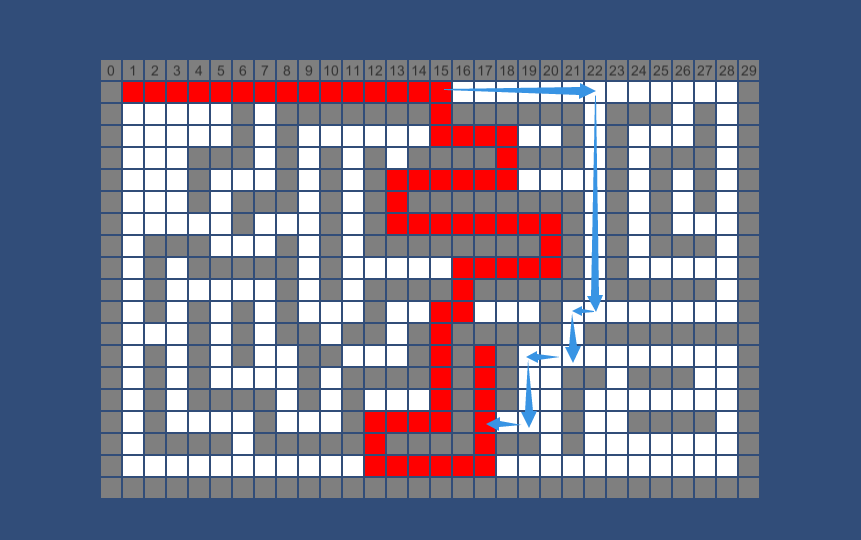
除此以外还有些展示算法的类,代码不在这里展出。下面是算法执行的截图,其中白色格子为可走的格子,灰色格子是不可穿越的,红色格子为查找到的路径,左上角格子为查找起点,右上角格子为查找终点。
后一个实例也展现了其"短视"的缺点,红线走了共65个格子,但蓝箭头方向只走了45个格子。
最后
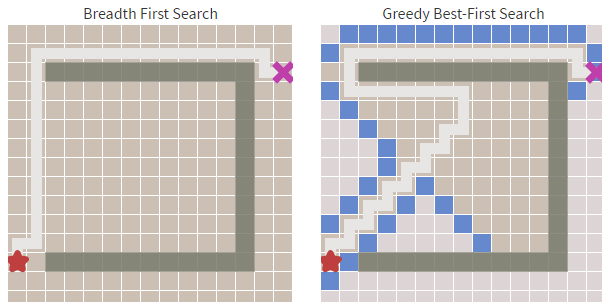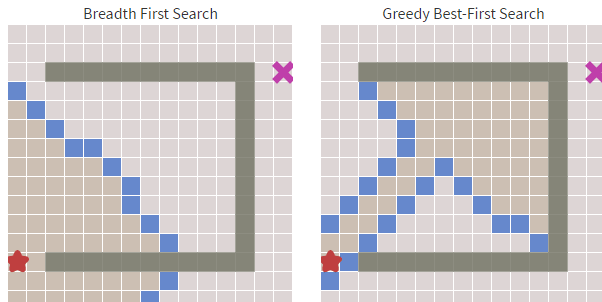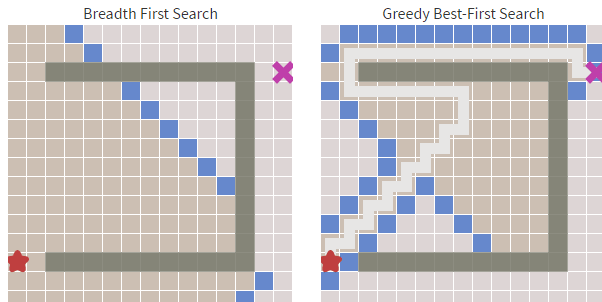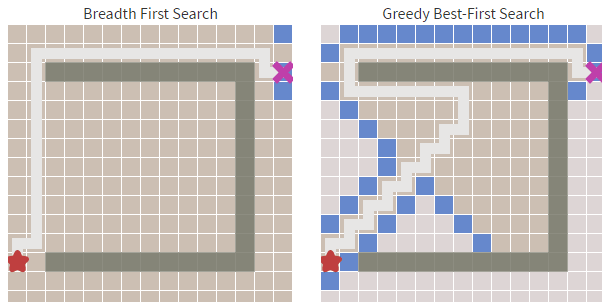
还有一种方案就是直接计算起点到终点的路径,这样可以节省一点计算开销。如下方右图,左图为广度优先算法。
本项目源码在 Github-PathFindingDemo 。
参考资料