Swift 算法查找篇笔记
未完工
尚缺 k-th Largest Element、Selection Sampling、Union-Find

简介
这是一系列关于Swift语言的算法笔记,Swift版本为3.0,参考的教程来自 Swift Algorithms Club 。
所有的代码可以直接在Xcode的Playground中运行,前面的算法较简单,主要说说算法的基础、思路和一些Swift语言的特性,我十分推荐你把这里的算法独自实现一遍。
另外这里可以下载 Swift Algorithms Club 算法教程的Epub文件! 点我下载
大 O 符号
大O符号(英语:Big O notation)是一种算法复杂度的相对表示方式。
这个句子里有一些重要而严谨的用词:
-
相对(relative):你只能比较相同的事物。你不能把一个做算数乘法的算法和排序整数列表的算法进行比较。但是,比较2个算法所做的算术操作(一个做乘法,一个做加法)将会告诉你一些有意义的东西。
-
表示(representation):大O(用它最简单的形式)把算法间的比较简化为了一个单一变量。这个变量的选择基于观察或假设。例如,排序算法之间的对比通常是基于比较操作(比较2个结点来决定这2个结点的相对顺序)。这里面就假设了比较操作的计算开销很大。但是,如果比较操作的计算开销不大,而交换操作的计算开销很大,又会怎么样呢?这就改变了先前的比较方式。
-
复杂度(complexity):如果排序10,000个元素花费了我1秒,那么排序1百万个元素会花多少时间?在这个例子里,复杂度就是相对其他东西的度量结果。
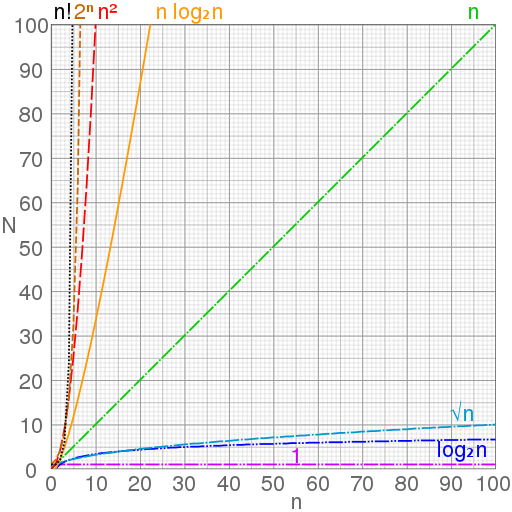
简单地说,O 表示法能给你一个算法的运行时间和它使用的内存量的粗略表示,这两种表示分为时间复杂度和空间复杂度,不过我们通常用 O 来表示时间复杂度,即一个算法执行的快慢。
| 大 O | 名字 | 说明 |
|---|---|---|
| O(1) | 常数 | 这是最好的。 该算法不管有多少数据,总是花费相同的时间。 示例:通过索引查找数组的元素。 |
| O(log n) | 对数 | 特别好。 该算法将每次迭代的数据量减半。 如果你有100个元素,它需要大约7个步骤来找到答案。 有1000个,需要10个步骤。 100万个只需要20步。 即使对于大量的数据,这也是超快的。 示例:二进制搜索。 |
| O(n) | 线性,次线性 | 很好。 如果你有100个元素,需要100个步骤。 元素个数增加一倍,该算法花费的时间会是两倍。 示例:顺序搜索。 |
| O(n log n) | 线性对数 | 体面的表现。 这比线性稍差,但不太差。 示例:最快的通用排序算法。 |
| O(n^2) | 平方 | 有点慢。 如果你有100个元素,要执行100 ^ 2 = 10,000步骤。 加倍的元素数量使其慢四倍(因为2平方等于4)。 示例:使用嵌套循环的算法,如插入排序。 |
| O(n^3) | 立方 | 很慢。 如果你有100元素,会是100 ^ 3 = 1,000,000步骤。 输入大小加倍使其慢8倍。 示例:矩阵乘法。 |
| O(2^n) | 指数 | 特别慢。 你想避免这些算法,但有时你没有选择。 添加一个元素就会使运行时间加倍。 示例:旅行推销员问题。 |
| O(n!) | 阶乘 | 无法忍受的慢。 一百万年也运行不完。 |
Linear Search
简介
Linear Search,又称线性查找、顺序查找。在给定的数组中,我们会遍历所有的元素,并逐个对比是否与要找的特定元素相等,找到即停止查找,返回特定元素的索引,反之继续遍历对比直至对比完最后一个元素。
目标:从一个数组查找到一个元素
代码
1 | func linearSearch<T: Equatable>(_ array: [T], _ object: T) -> Int? { |
放进playground中测试:
1 | let array = [5, 2, 4, 7] |
这是最简单的一个查找了,这里说说Swift的语言特性。
<T: Equatable> 中 T 指泛型,而 Equatable 是Swift标准库中定义的一个协议,该协议要求任何遵循该协议的类型必须实现等式符 == 及不等符 !=,从而能对该类型的任意两个值进行比较。所有的 Swift 标准类型自动支持 Equatable 协议。
Int? 中的 ? 是指返回的值是 Optional 的,如果查找找到值就返回索引值,找不到就返回 nil,Optional 特性让一个值能同时兼容两种情况。
enumerated()是一个实例方法,返回的是键值对 (n, x),n 表示一个连续的从0开始的正整数,x 表示对应的元素。
1 | let array = [5, 2, 4, 7] |
性能
线性查找的效率是O(n)^Big O notation。在最差的情况,我们需要把全部元素都比较一边,最好的情况是我们第一次就查找到相同元素。
Binary Search
简介
Binary Search,就是著名、高效并应用广泛的二分查找算法。
目标:快速地从一个数组查找到一个元素
代码
通常情况下,Swift 的indexOf()方法已经足够好了:
1 | let numbers = [11, 59, 3, 2, 53, 17, 31, 7, 19, 67, 47, 13, 37, 61, 29, 43, 5, 41, 23] |
内置的indexOf()方法实现了一个线性查找,实现方式类似以下代码:
1 | func linearSearch<T: Equatable>(_ a: [T], _ key: T) -> Int? { |
测试:
1 | linearSearch(numbers, 43) // returns 15 |
这代码其实和一开始的线性查找差不多,但是线性查找效率不太高,平均都要搜索半个数组,如果数组足够大,查找将会变得很慢。
分而治之
凡邦之有疾病者,疕疡者造焉,则使医分而治之,是亦不自医也。
──清·俞樾《群经平议·周官二》
分而治之方法与软件设计的模块化方法非常相似。为了解决一个大的问题,可以:
- 把它分成两个或多个更小的问题
- 分别解决每个小问题
- 把各小问题的解答组合起来,即可得到原问题的解答。小问题通常与原问题相似,可以递归地使用分而治之策略来解决。
在本算法中,我们需要用这策略去不断的拆分数组,直到找到特定元素。另外二分查找的效率是O(log n),也就是对一个有着1,000,000个元素的数组只要将近20步就能找到特定元素,因为log_2(1,000,000) = 19.9,十亿个元素也只需要30步就能完成查找!
听起来爽,但是二分查找有个缺点,就是数组必须是排序好的,不过这通常不是一个问题。
二分查找是怎么操作的呢?
- 把排序好的数组平分成两部分,把特定元素与中间键比较,看特定元素应该会在数组左部分(较小)、右部分(较大)或直接相等。
- 如果在数组左部分,则把数组切剩下左部分,继续进行二分查找。
- 这里使用了递归,切分的是数组范围
range
先来看看代码吧:
1 | func binarySearch<T: Comparable>(_ a: [T], key: T, range: Range<Int>) -> Int? { |
测试1:
1 | let numbers = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67] |
测试2:
1 | let numbers = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67] |
这其中使用了 Comparable 协议,没有这协议,泛型和其他值是不能比较的, Comparable 协议就是说明T是可比较的。
测试1中用线性查找的话要查找13次,测试2中用线性查找要查找19次,而二分查找分别只用4次和5次就完成查找,能感受算法的威力吗~
迭代和递归
二分查找是递归的因为我们每次查找都是相同的逻辑,当然用迭代去实现将会更加有效率,因为不需要一次一次地调用函数(考虑下内存空间!)。
1 | func binarySearch<T: Comparable>(_ a: [T], key: T) -> Int? { |
测试:
1 | let numbers = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67] |
最后
由于数组必须要先排序,排序和查找的时间加在一起算的话,二分查找耗时可能比顺序查找还多,因此二分查找适合在那种只用排序一次而要查找很多次的情况。
Count Occurrences
简介
Count Occurrences 就是计数,有时候我们需要计算一个数字出现的次数。当然我们可以用线性查找从头查到尾,这样这种计数的效率是O(n),当然如果我们修改一下二分查找,也能把计数的效率提高到O(log n),别忘了二分查找的条件是数组排序好。
目标:计算一个特定元素在一个排序好的数组中出现的次数
代码
1 | func countOccurrencesOfKey(_ key: Int, inArray a: [Int]) -> Int { |
测试:
1 | let a = [ 0, 1, 1, 3, 3, 3, 3, 6, 8, 10, 11, 11 ] |
这里使用二分查找方式计数的技巧就是找到特定元素出现的左右边界,当然我们这次要查找的不是特定元素3,而是索引为2的1(左边界)和索引为7的6(右边界)。我们通过不断把左边界和特定元素比较,在第n-1次查找中,范围中的数组upperbound就是左边界,同理右边界在第n-1次查找中,范围中的数组lowerbound就是右边界。如果左边界和右边界都返回0,则代表找不到特定元素。
这是运用算法解决问题的一次实践。
跑个题,我在高中的时候是个小课代表,老师通常会把一叠改好的按学号排序的试卷交给我发放给全班同学。我记得同学各自的学号,查找的时候我会估摸着同学的学号,然后在一叠试卷中的相应位置抽出一张来。不是,放进去,试卷对应的学号小了,我就继续往后估摸位置再抽一张,直到找到为止,这很像二分查找吧!
Select Minimum / Maximum
最大值或最小值
Select Minimum / Maximum,选择最小值或最大值,也是我们会遇到的情况。
目标:在一个未排序的数组中找到最小值或最大值
🌰
举个栗子,我们要在一个未排序的数组[ 8, 3, 9, 4, 6 ]中找到最大值。
- 找到第一个元素
8,存储为最大值 - 找到下一个元素
3,比较现有最大值8,3<8,所以最大值8不变 - 找到下一个元素
9,比较现有最大值8,9>8,所以最大值赋值为9 - 重复步骤直到所有元素遍历一遍
最小值和以上步骤类似,每次储存较小值即可。
代码
1 | func minimum<T: Comparable>(_ a: [T]) -> T? { |
测试:
1 | let array = [ 8, 3, 9, 4, 6 ] |
Swift标准库
然而 Swift 标准库已经给我们提供了查最大值或最小值的方法
1 | let array = [ 8, 3, 9, 4, 6 ] |
最大值和最小值
如果我们要同时查找最大值和最小值呢?
🌰
如果我们要同时在一个未排序的数组[ 8, 3, 9, 6, 4 ]同时查找最大值和最小值,我们需要两两比较其中的元素。
- 找到第一个元素
8,同时存储为最大值和最小值 - 由于数组中有奇数个数组,当移除元素
8之后,剩下[3, 9]和[6, 4]这两对子数组 - 在第一个子数组
[3, 9]中,比较两数大小。3较小,与当前最小值8比较,3<8,因此把最小值赋值为3。9较大,与当前最大值8比较,9>8,因此把最大值赋值为9。 - 第二个子数组
[6, 4]中,比较两数大小。4较小,与当前最小值3比较,4>3,因此最小值不变。6较大,与当前最大值9比较,6<9,因此最大值不变。 - 最大值为9,最小值为3。
代码
1 | func minimumMaximum<T: Comparable>(_ a: [T]) -> (minimum: T, maximum: T)? { |
测试:
1 | let array = [ 8, 3, 9, 4, 6 ] |
hasOddNumberOfItems确保数组一直能够被两两分组,实际上数组元素在 while 循环中一直在被两个两个地 remove,同时在做比较大小并赋大小值。
k-th Largest Element Problem
简介
k-th Largest Element Problem,是查找一个数组中第 k 个较大的元素的问题。
例如,第一个较大的元素是数组中的最大值,如果数组有 n 个元素,那么第 n 个较大的元素就是该数组的最小值,中位数就是第 n/2 个较大的元素。
naive solution
下面的算法是 semi-naive (较幼稚…?)的,从第一次排序好数组后,时间复杂度为O(n log n),并且额外用了 O(n)的空间复杂度。
1 | func kthLargest(a: [Int], k: Int) -> Int? { |
在这方法中,a 是接受输入的数组,k 是返回第 k 个较大的数。
举个例子,设 k = 4,输入数组为
[ 7, 92, 23, 9, -1, 0, 11, 6 ]
一开始没有直接的办法去找第 k 个较大的数,首先我们需要排序好数组。
[ -1, 0, 6, 7, 9, 11, 23, 92 ]
现在我们需要拿到索引为a.count - k的元素。
a[a.count - k] = a[8 - 4] = a[4] = 9
当然了,如果要找第 k 个较小的数,我们会用a[k]。
A faster solution
这里有一种结合了二分查找和快速排序的算法,时间复杂度能达到 O(n)。
还记得二分查找不断的划分一半数组吗?这样能快速地靠近要查找的元素,这里我们也需要这么做。
快速排序也划分数组,它把所有较小的元素移到中轴的左边,较大的元素放在右边。








