2020年7月26日更新:
最近对变换重新学习整理了,文章在:图形学常见的变换推导。
上一篇笔记3D 数学基础-向量运算基础和矩阵变换记录了一些向量和矩阵运算的基础,和一些矩阵基本的变换。这篇笔记主要介绍了平移变换、齐次坐标、平移和旋转变换的组合、法线变换和改变坐标系。
平移(Translation)
前一篇文章总结了旋转、缩放等变换,这里介绍一下平移变换。
假如我们需要把 X 坐标从 x 变换到 x + 5,我们需要构造什么样的变换矩阵来实现平移呢?
x′y′z′=?xyz=x+5yz
要注意的是,变换矩阵不能包含 x、y、z 等坐标变量。例如要得到 x + 5,那么矩阵的第一个行向量不能是 $$(1, 0, 5/z)$$,因为变换的一个重要性质是变换矩阵保持不变。
我们可以给矩阵多加一个维度 w,令其等于 1,这样就不需要用到 x、y、z 这些坐标变量了。
x′y′z′w′=1000010000105001xyz1=x+5yz1
这里引用到了齐次坐标的概念。
齐次坐标
齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射几何变换。
—— F.S. Hill, JR 《计算机图形学(OpenGL 版)》作者
想要了解三维坐标是怎么样扩展到四维坐标,可以先了解下二维空间中的齐次坐标 $$(x, y, w)$$。
下图的三维坐标中在 $$w=1$$ 处有一个二维平面,则该平面上的二维平面坐标可以表示为 $$(x, y, 1)$$,图中的 $$(1.0, 0.8, 1.0)$$ 就是一个在该二维平面上的点。对于不在二维平面上的点,我们则将其投影到二维平面上,所以齐次坐标 $$(x, y, w)$$ 映射到实际二维平面上的点为 $$(x/w, y/w)$$,例如另外一个点 $$(2.5, 2.0, 2.5)$$ 在 $$w=1$$ 二维平面投影得到的点为 $$(1.0, 0.8)$$。
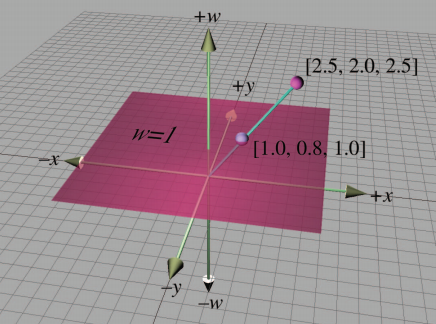
同理,三维空间的点可以认为是在四维空间中 $$w=1$$ 的“平面”上,所以齐次坐标 $$(x, y, z, w)$$ 映射到三维空间上的点为 $$(x/w, y/w, z/w)$$,这也就是点的非齐次坐标。
xyzw=x/wy/wz/w1
四维齐次坐标的任何常量缩放会得到相同的结果,也就是说,它包含了点的非齐次坐标所有可能的缩放(还记得上面图中的两个点吗?),w 可以等于任何数值:
- 如果 w > 0,这表示一个真实物理世界的点,我们可以用 x,y,z 三个坐标除以 w 得到这个真实的点。
- 如果 w = 0,这表示一个无穷远处的点。在实际应用中,通常表示一个向量。
齐次坐标的优点:
- 让我们可以同时考虑所有的变换,如平移、观察、旋转、透视投影等。(如果我们要做缩放变换,可以直接变换 x、y、z 的值并且保持 w 不变。)
- 整个渲染管线都以 4 * 4 的齐次坐标矩阵以及对应的四维向量为基础,只有在最后要表示真实点的位置的时候,才需要把齐次坐标变为非齐次。(计算机里除法是个非常复杂的操作,需要花费更多的时间周期,但齐次坐标只需在渲染管线最后一步做除法。)
- 不会出现特殊情况。有时考虑判断直线是否相交,当它们平行的时候,有些公式会出错,但无穷远点已经在齐次坐标中约定了 w=0。
- 四阶矩阵和齐次坐标是计算机图形软件和硬件中普遍使用的标准。
下面表示的是一个点向量加上一个平移变量:
P′=TP=100001000010TxTyTz1xyz1=x+Txy+Tyz+Tz1=P+T
有时候平移矩阵 T 内的左上角部分会直接用单位矩阵来表示,其中 $$I_{3}$$ 表示 3 * 3 的单位矩阵。
T=100001000010TxTyTz1=[I30T1]
组合平移和旋转变换
当要对一个点进行两种变换的时候,就会涉及到变换顺序的问题,是先平移再旋转,还是先旋转再平移?
先旋转再平移
P′=(TR)P=MP=RP+T
其中 T 为平移矩阵,R 为旋转矩阵,矩阵 P 通过平移再旋转后得到矩阵 P’。注意,在上面的公式中做的是标准的向量计算,在计算时才用齐次坐标计算。
由于我们使用的是列矩阵,矩阵的阅读顺序应该从右到左。也就是说对于 TR 这个旋转矩阵而言,(TR)P 这个操作,就是对矩阵 P 先 R 旋转,再进行 T 平移。
M=100001000010TxTyTz1R11R21R310R12R22R320R13R23R3300001=R11R21R310R12R22R320R13R23R330TxTyTz1=[R0T1]
MP=[R0T1][P001]=[RP0T1]=RP+T
先平移再旋转
P′=(RT)P=MP=R(P+T)=RP+RT
M=R11R21R310R12R22R320R13R23R3300001100001000010TxTxTx1=[R3×301×3R3×3T3×11]
MP=[R3×301×3R3×3T3×11][P001]=[RP0RT1]=RP+RT
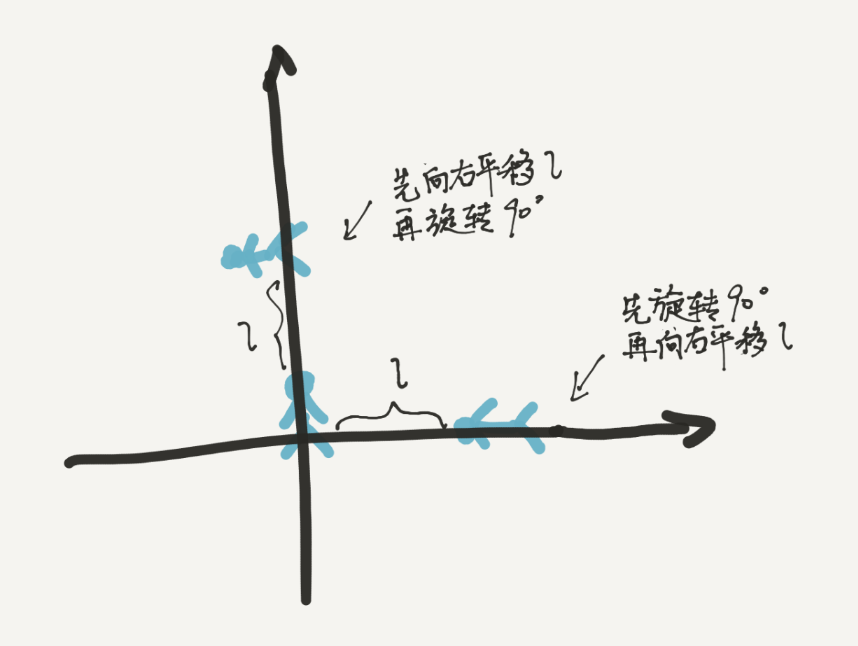
对比先平移再旋转的结果,可以看到不同的地方是 T 变成了 RT,也就是说旋转也施加在了平移的方向上。在下图中可看到小人在 Y 轴方向发生了平移,所以先旋转再平移可能会更容易得到理想的结果,但两种变换组合都是可行的。(在 gluLookAt 的推导中需要先做平移,gluLookAt 是 OpenGL 中观察变换的一个关键函数。)
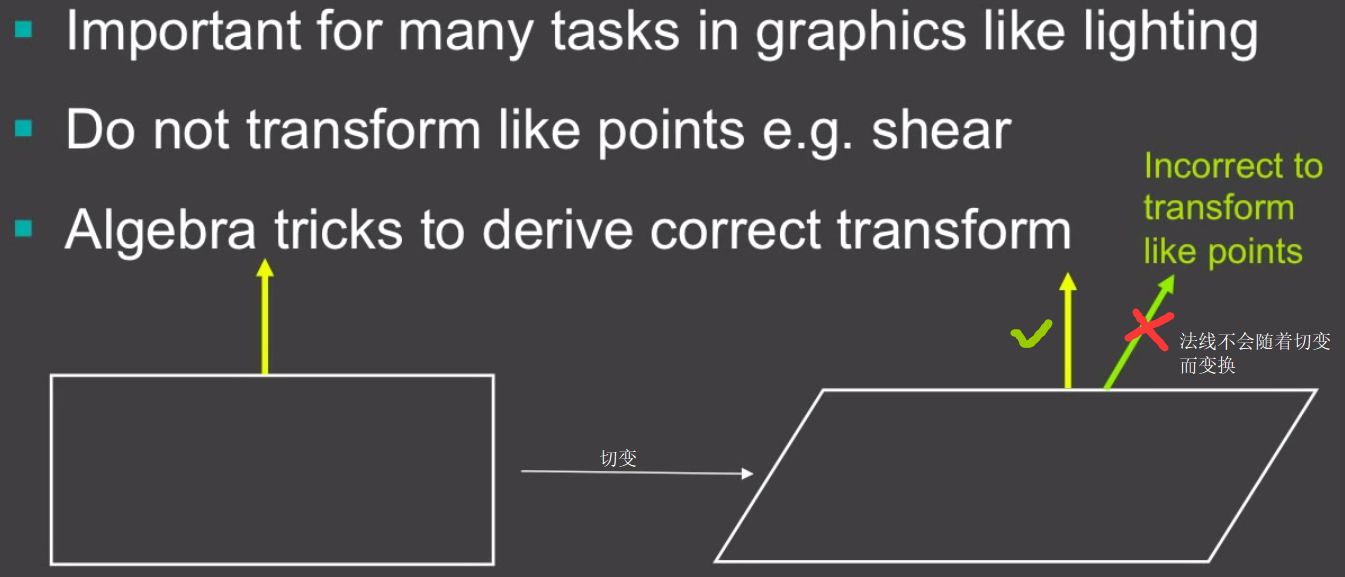
法线变换
在图形学中曲面法线的方向也很重要。
法线(Normal)
法线是始终垂直于某平面的虚线。在数学几何中法线指平面上垂直于曲线在某点的切线的一条线。
——百度百科
切线的位置实际上就是曲面上的几何位置,因此它们的变换矩阵和曲面的变换矩阵保持一致。
t→Mt
而法线变换是另外一个矩阵,我们称之为 Q。
n→Qn Q=?
法线必须垂直于这些切线,因此法线和切线的点积等于 0。
nTt=0
变换后法线和切点依然互相垂直,可得:
(Qn)T=(nTQT)(Mt)=0
在该等式中,只有当 $$Q^{T}M=I$$ 时,矩阵才容易求解。
nTQTMt=0⇒QTM=I
最后可得法线变换公式,其中 $$M^{-1}$$ 只对左上角的 3 * 3 矩阵求逆和转置:
Q=(M−1)T
要进行法线变换,这个公式要施加在曲面上所有的法线上。
另外要注意的是法线是一个向量,不会随着平移而改变,因此平移变换对法线没影响。
改变坐标系
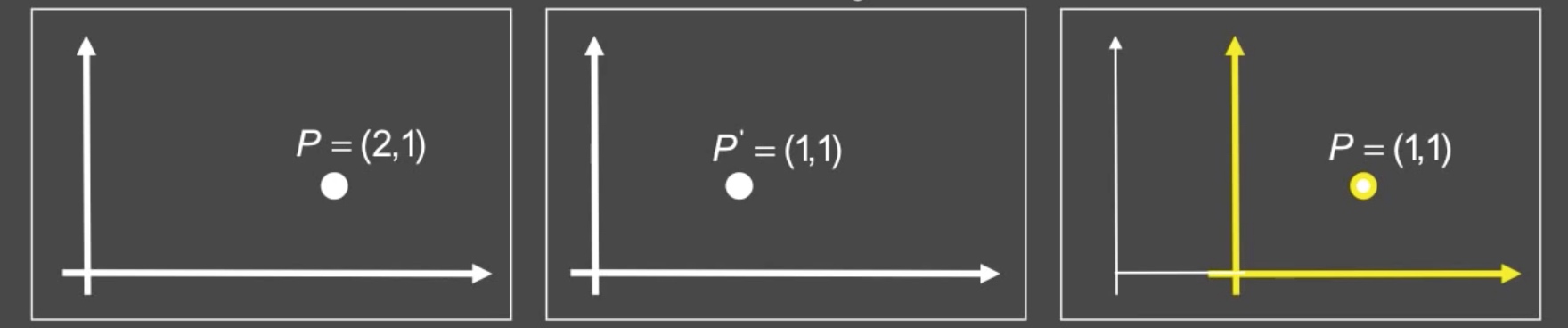
在图中,点 (2, 1) 要平移到 (1, 1) 处,可以直接把点向左平移,也可以看成是坐标系的改变,将坐标系向右平移。
引出坐标系的概念是因为,在很多情形下,我们需要一个特定的物理位置在不同的坐标系间变换,例如上一篇文章正交坐标系中所举的例子。下图中,有世界坐标系、相机坐标系和点 P。
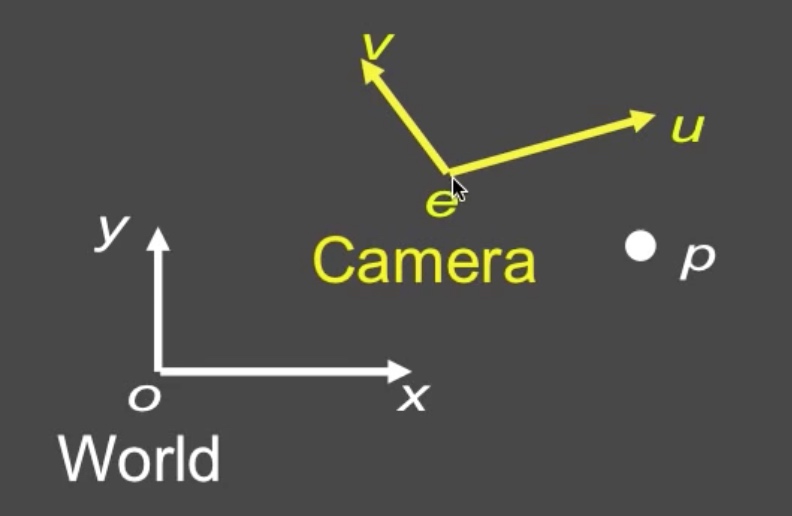
点 P 在两个坐标系中的坐标是不同的,而在图形学中,我们经常要做这样的变换。
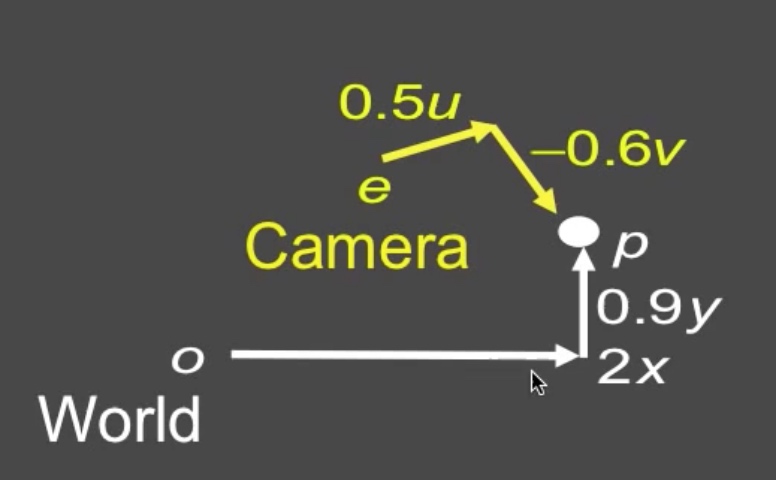
如果我们在世界坐标系中有一个点,要计算出其在相机坐标系中的位置,则要同时考虑相机旋转的坐标系、相机的位置和观察的位置(视点)。
在二维空间下的旋转中能看到二维旋转矩阵的推导过程,在此基础上,可以看作坐标系向右旋转了θ度,这样点 P 就在新坐标系中到达目标位置 P’ 了。
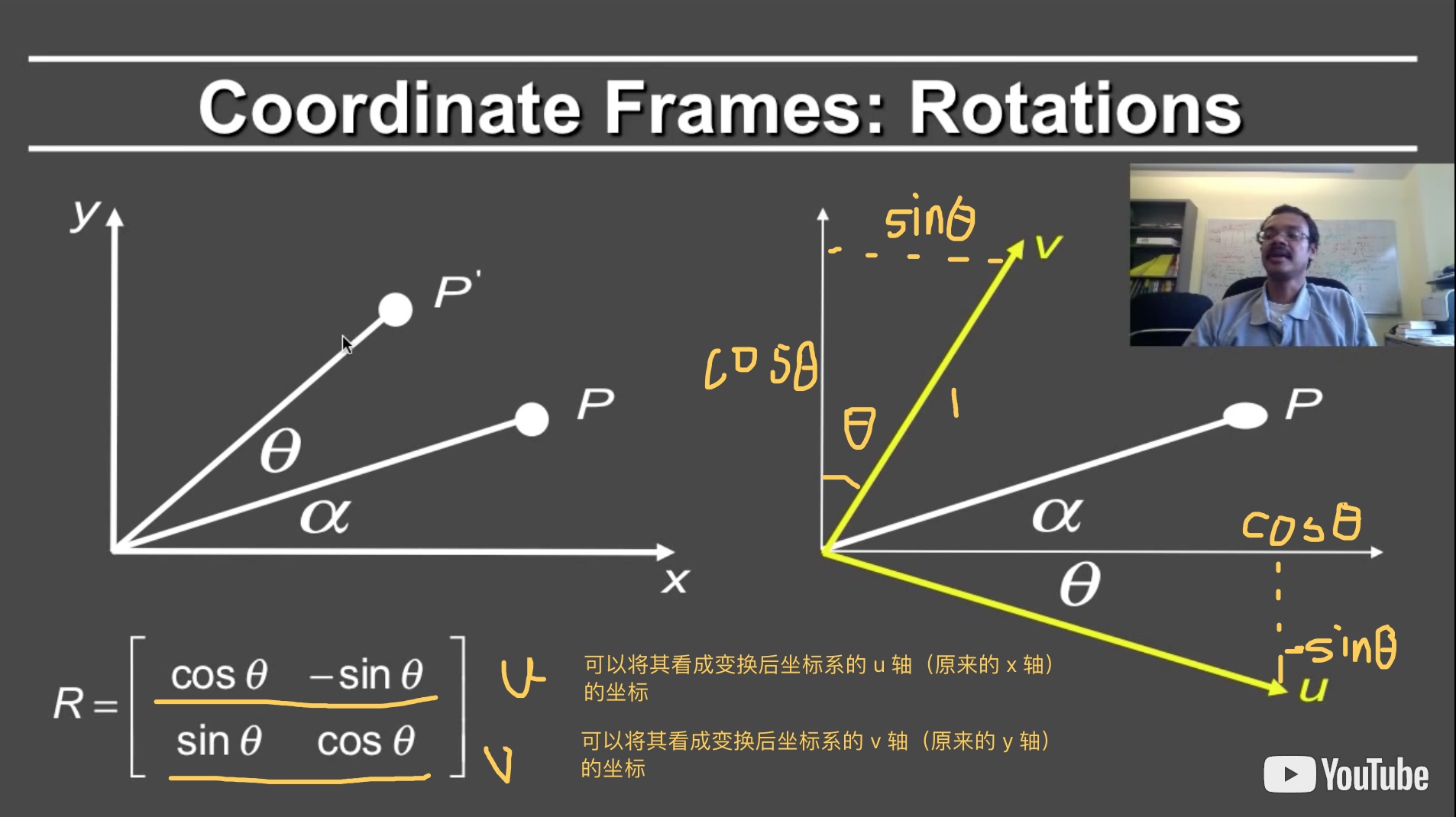
这样我们就能通过旋转矩阵来得到新的 uv 坐标系了!
[uv]=[cosθsinθ−sinθcosθ][xy]
之前讨论的都是三维的变换,下篇笔记会介绍图形学中的观察(Viewing)。3D 数学基础知识有点枯燥,但这是入门图形魔法的必经之路。
参考资料
















