图形学常见的变换推导
注意:由于这个博客主题对 MathJax 支持不好,部分推导转用图片代替,或者可以移步我的 Notion 笔记:Transformation。
本文是 Games101-现代计算机图形学入门 第三和第四节课的笔记,文中对二维变换、三维变换、视图变换、正交投影和透视投影做了推导,相关视频在下方。
GAMES101-Lecture03 Transformation
GAMES101-Lecture04 Transformation Cont.
本文同时参考了《Unity Shader 入门精要》的第四章,作者公开了第四章的 PDF,可以在下面下载到。
candycat1992/Unity_Shaders_Book
闫老师的推导十分简洁易懂,我也尽量把过程补充到文章中,读者看了我相信肯定也能跟着思路把变换公式推导出来。
在读本文的过程中,也推荐参考上面提到的视频和 pdf 互相参考,本文是视频中推导的详细笔记,冯乐乐的 pdf 中虽然没有投影变换的推导,但是在很多地方都把理论讲的十分清晰,例如必要的数学基础和各种图形学概念的讲解。
线性变换
如果我们可以把变换写成这样一种形式,矩阵乘以输入坐标等于输出坐标,这样可以叫做线性变换。
Scale Matrix
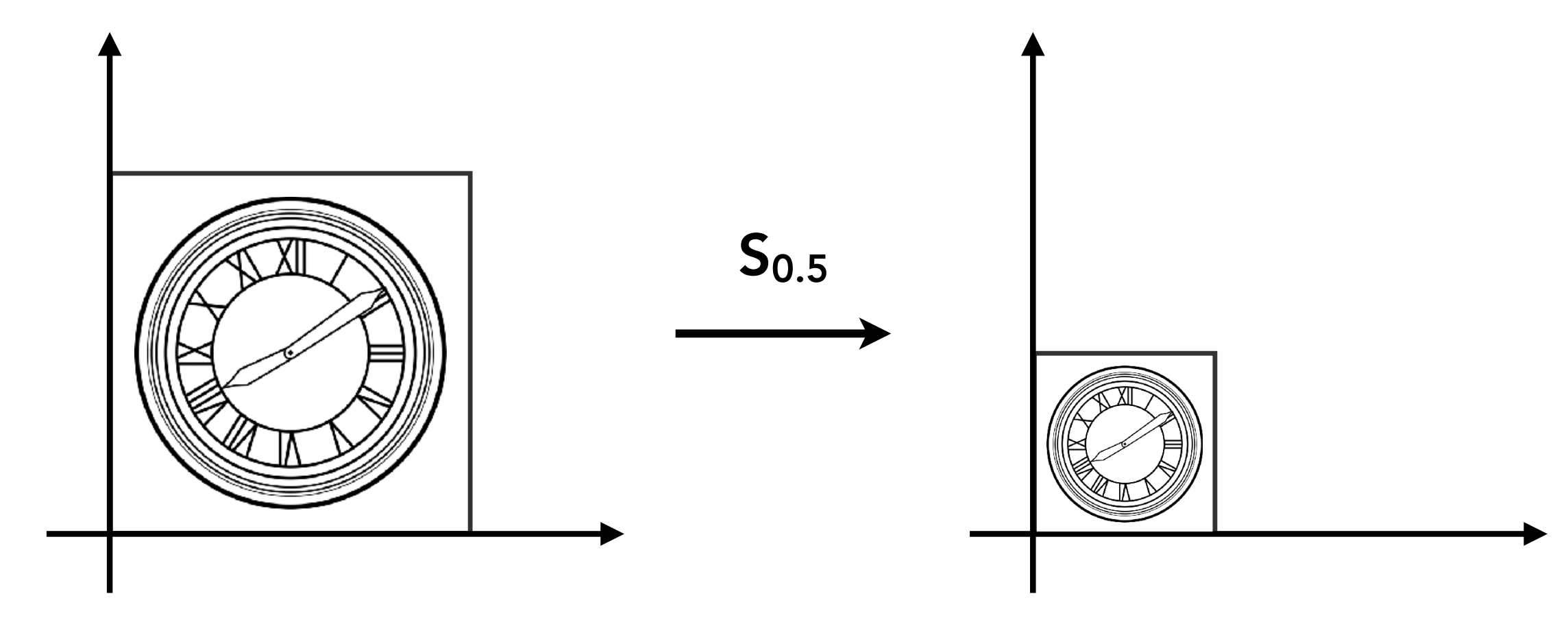
其变换矩阵:
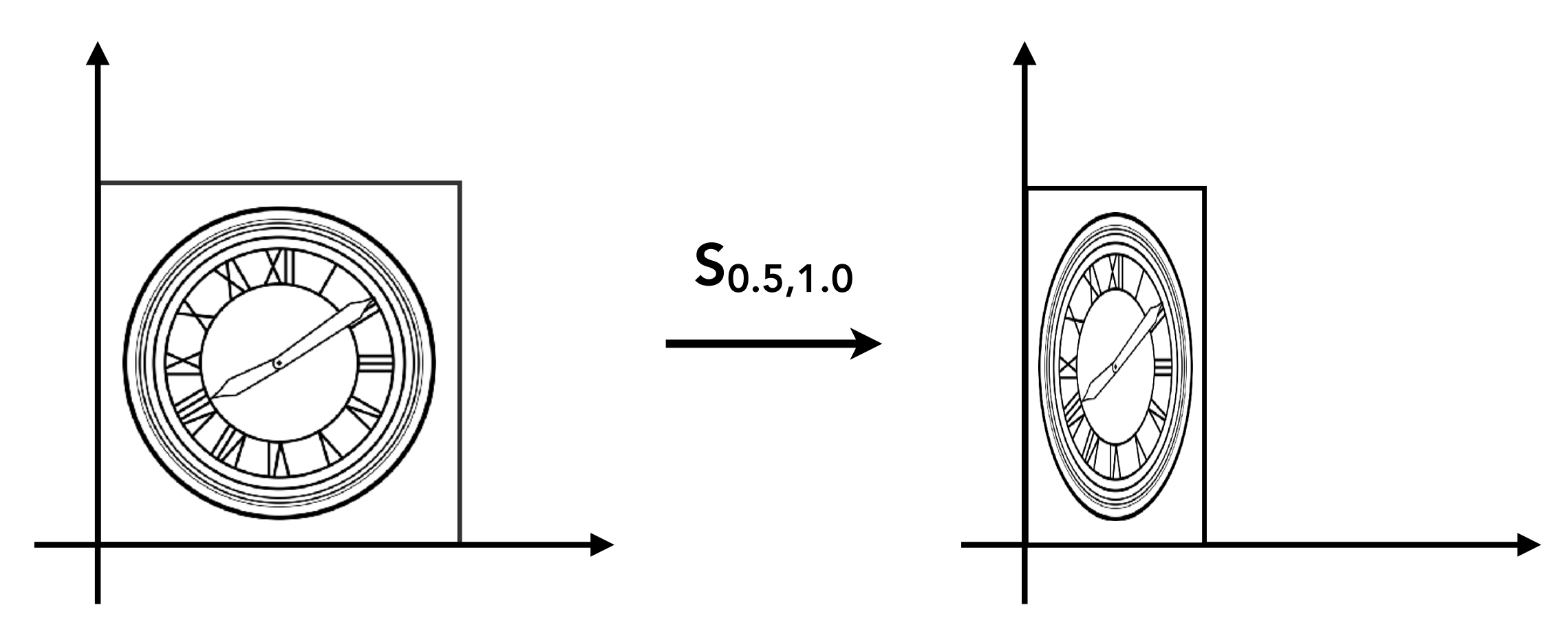
Scale (Non-Uniform)
x y 可以不均匀地缩放
Reflection Matrix
Horizontal reflection:
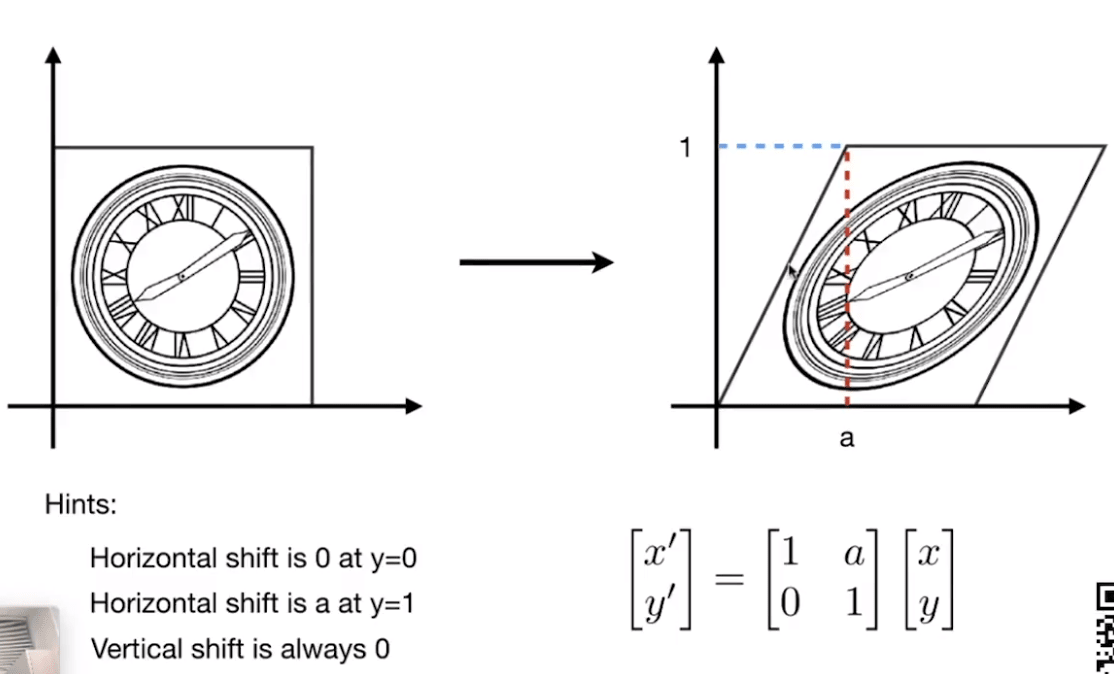
Shear Matrix
2D Rotation Matrix
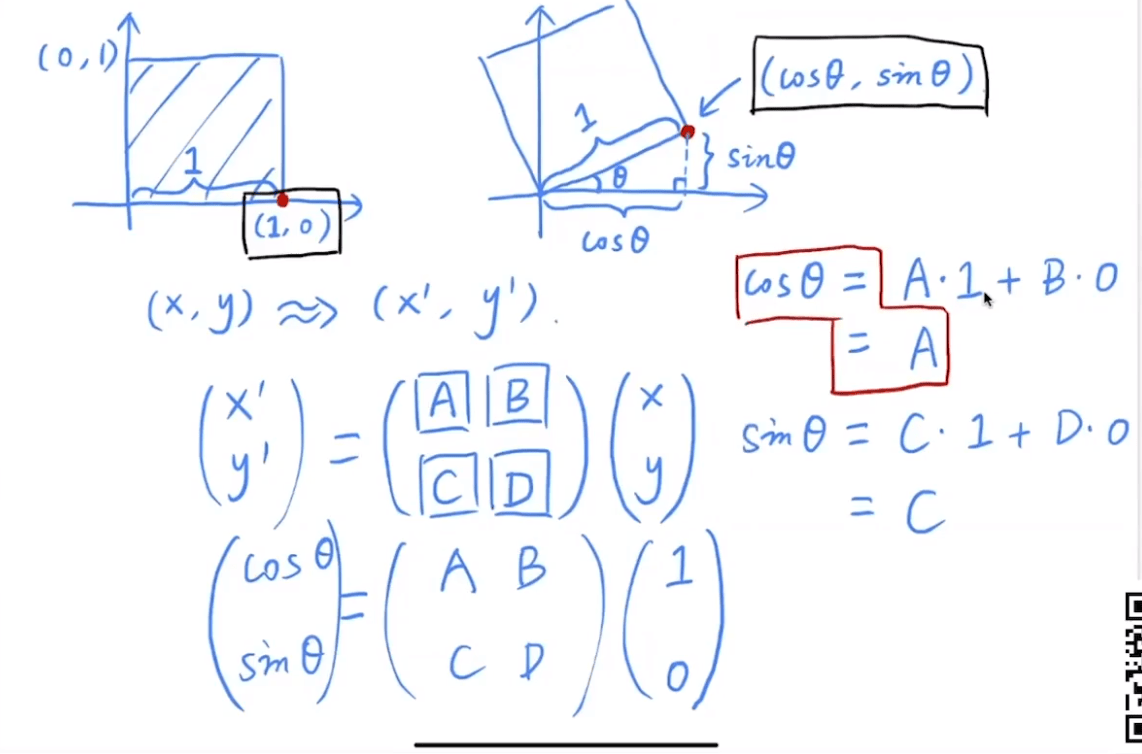
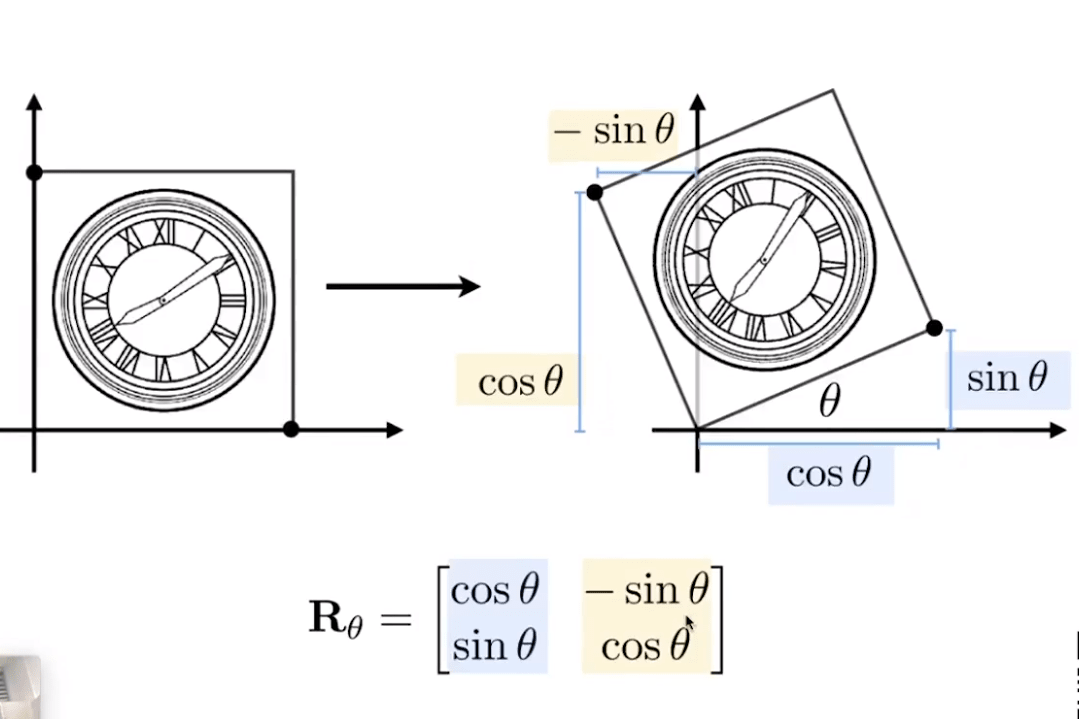
齐次坐标
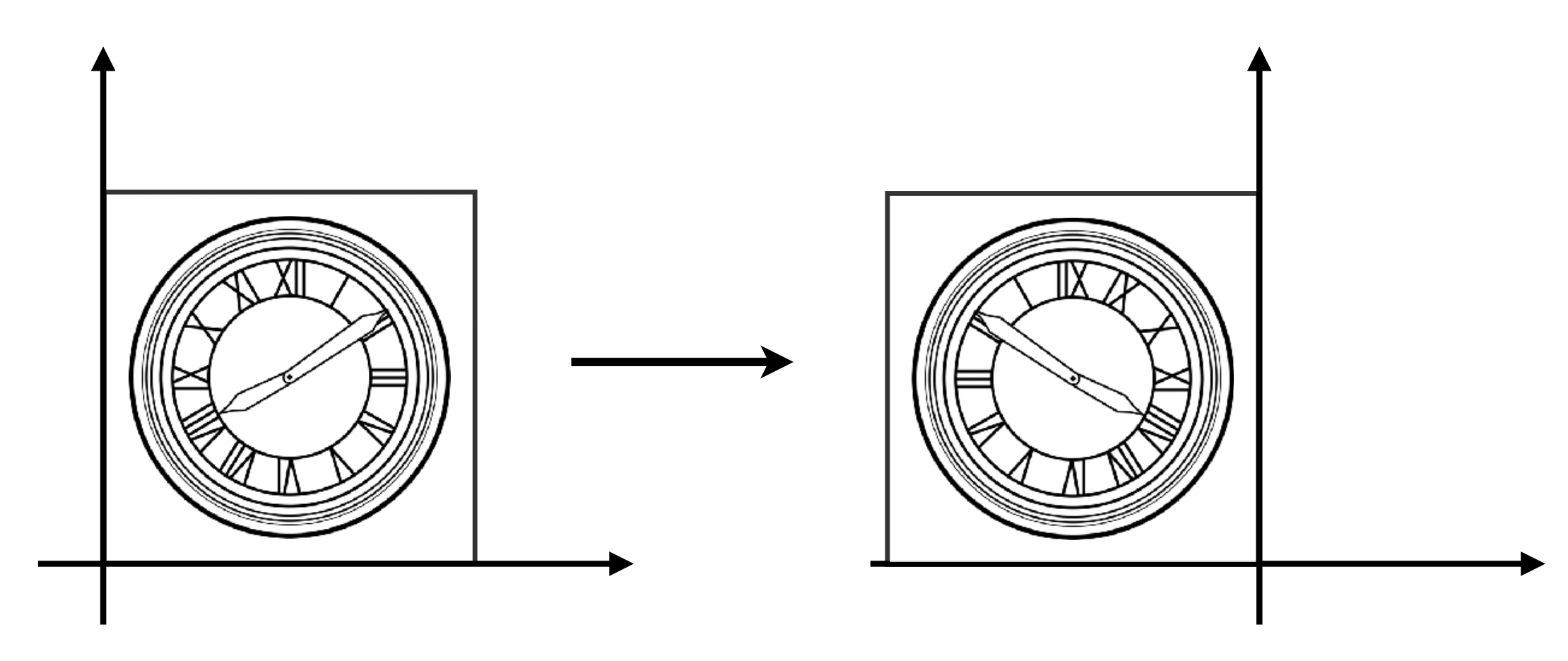
Translation
平移变换非常特殊。
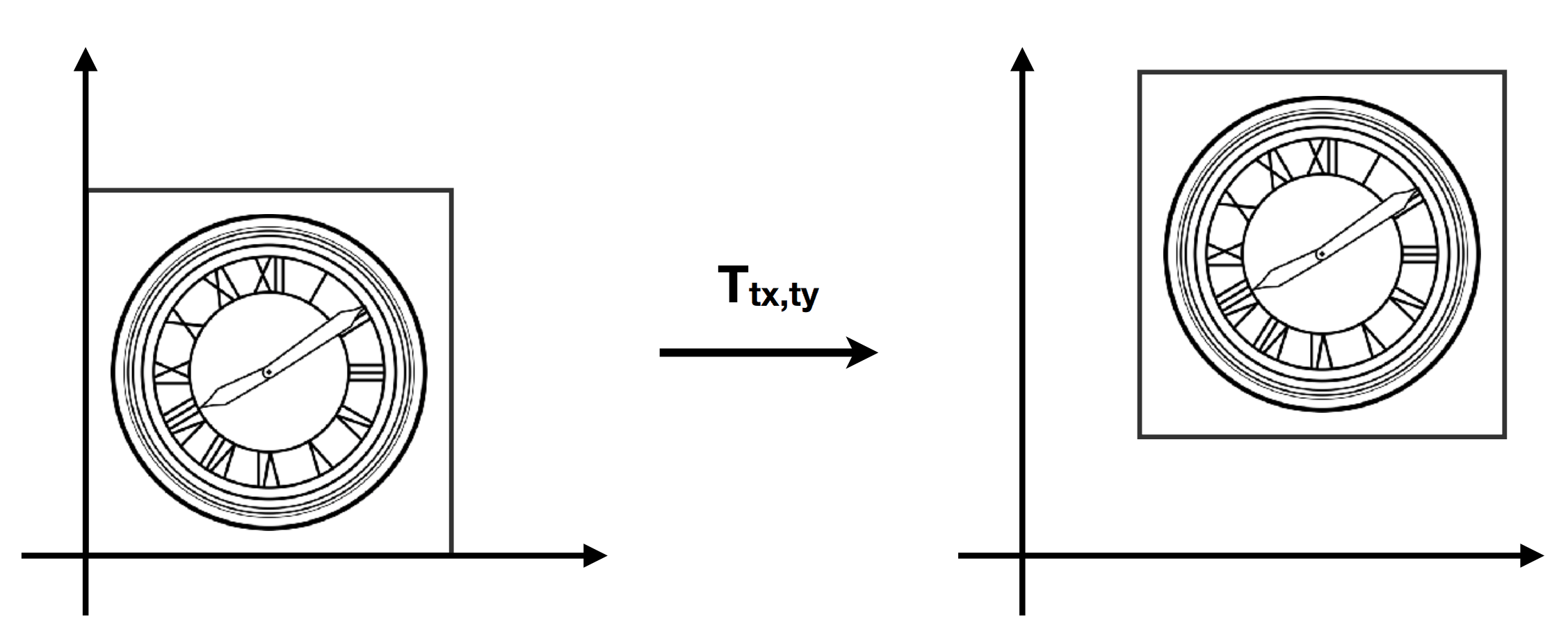
写出来简单,但是两个式子不能写成线性变换的形式。
只能写成:
因此平移变换并不是线性变换。
但是我们不希望将平移变换看作一个特殊的例子,那么有没有办法将缩放、错切、平移等变换用一种统一的方式来表示?
在计算机科学,永远要考虑 “Trade-Off”。数据结构中不同降低时间复杂度的办法都会引入空间复杂度。如果两者都能低就很好,但更多时候是非此即彼的事情。“No Free Lunch Theory”。

引入齐次坐标,可以通过增加一个维度来将平移变换也写成矩阵乘一个点的形式。
向量具有平移不变性,因此后面是 (x, y, 0),平移变换后也不变。
我们也可以通过 w 分量来推出我们操作的结果:
Valid operation if w-coordinate of result is 1 or 0
- vector + vector = vector
- point – point = vector
- point + vector = point
- point + point = ??
Affine Transformations 仿射变换
Affine map = linear map + translation
Using homogenous coordinates:
2D Transformations
Scale
Rotation
Translation
逆变换
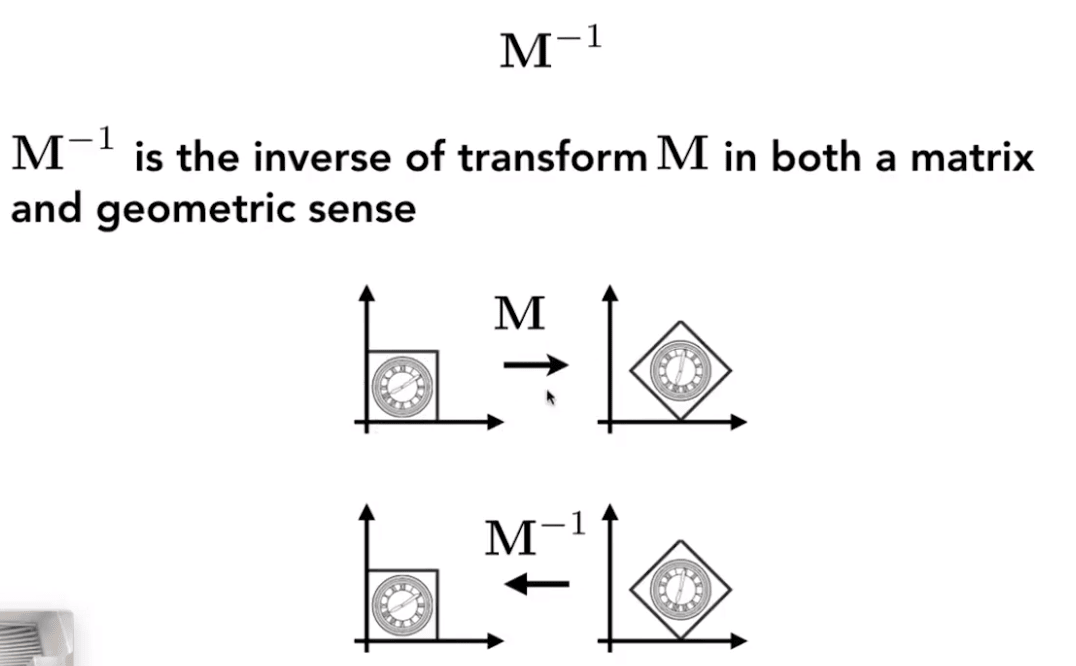
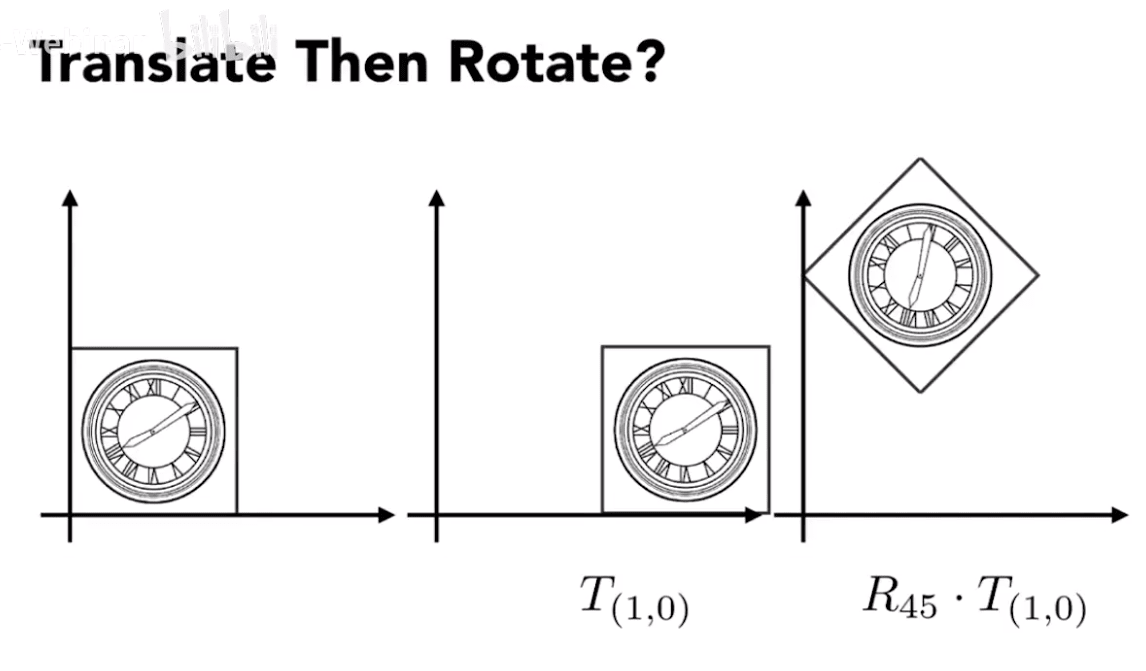
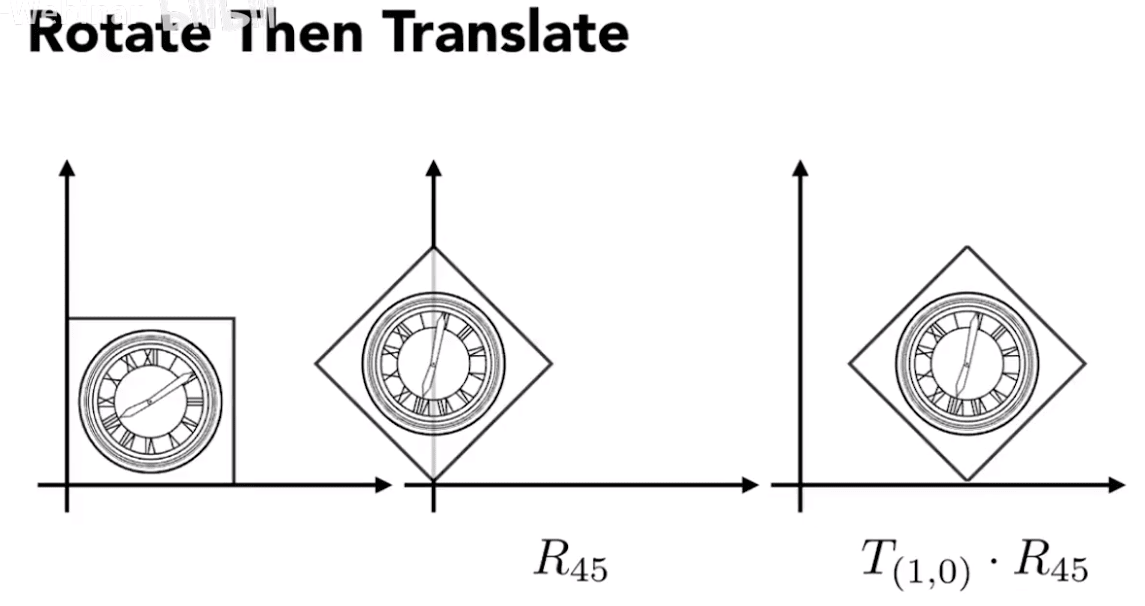
因此变换顺序是很重要的,不满足交换律。
矩阵是从右到左运算的:
矩阵没有交换律,但有结合律。

三维变换
齐次坐标系下的三维变换可以写成下面的形式
Scale
Translation
Rotation
绕轴旋转
Rotation around x-, y-, or z-axis
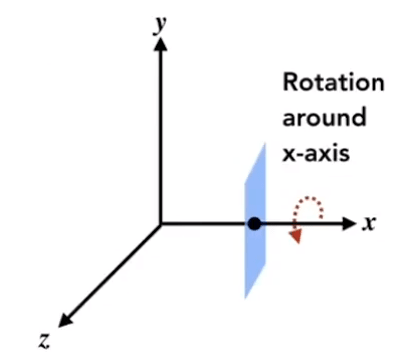
绕着 x 轴旋转,说明 y 和 z 都是在进行旋转的,但 x 不变。因此绕 x 轴的旋转矩阵相比二维的旋转矩阵,第一行是不变的。中间部分和二维旋转矩阵一样。
绕 y 轴旋转不一样,这里涉及到我们要如何思考轴的相互顺序。
根据右手螺旋定则,x 叉乘 y 得到 z,y 叉乘 z 得到 x。但 z 叉乘 x 才能得到 y,是反的,因此 Ry 部分不一样。
Rodrigues’ Rotation Formula
我们能够解决一些简单的问题,复杂的问题可以转化成一些简单问题的组合。
给定根据三个轴的旋转,能否将某一个方向旋转到任意一个方向上去?
Rotation by angle α round axis n
有人将任意一个旋转分解成通过 x y z 轴分别做旋转。
证明过程可以参考闫令琪老师的证明:
公式给了我们一个旋转矩阵,定义中给了我们一个旋转轴 n 和旋转角度 α。旋转角度好理解,但旋转轴似乎不能这么简单地定义。因为一个旋转轴首先跟起点有关系,然后跟方向有关系,只给一个向量是不是不太合适?
假如说沿着 y 轴旋转,跟沿着 x 和 n 各等于 1 并且也是沿着 y 方向的向量。方向一样,但起点不一样,结果肯定也是不一样的。因此我们说沿着某个轴的方向旋转,就默认了是过原点的,这样起点就在原点上,方向就是 n 方向。
那么如果轴 n 可以平移怎么办?那么我们可以将其进行变换的分解。如果我们要沿着任意轴旋转且轴的起点不在原点,我们可以将所有的东西移到起点为原点的条件下,再旋转,再移回去。
四元数相关
我们上面所用到的旋转矩阵是不太适合做插值的,例如二维旋转 10 度的旋转矩阵加二维旋转 20 度的旋转矩阵求平均,不能得到二维旋转 15 度的旋转矩阵。四元数在这方面方便很多。
View/Camera Transformation 视图变换
定义相机
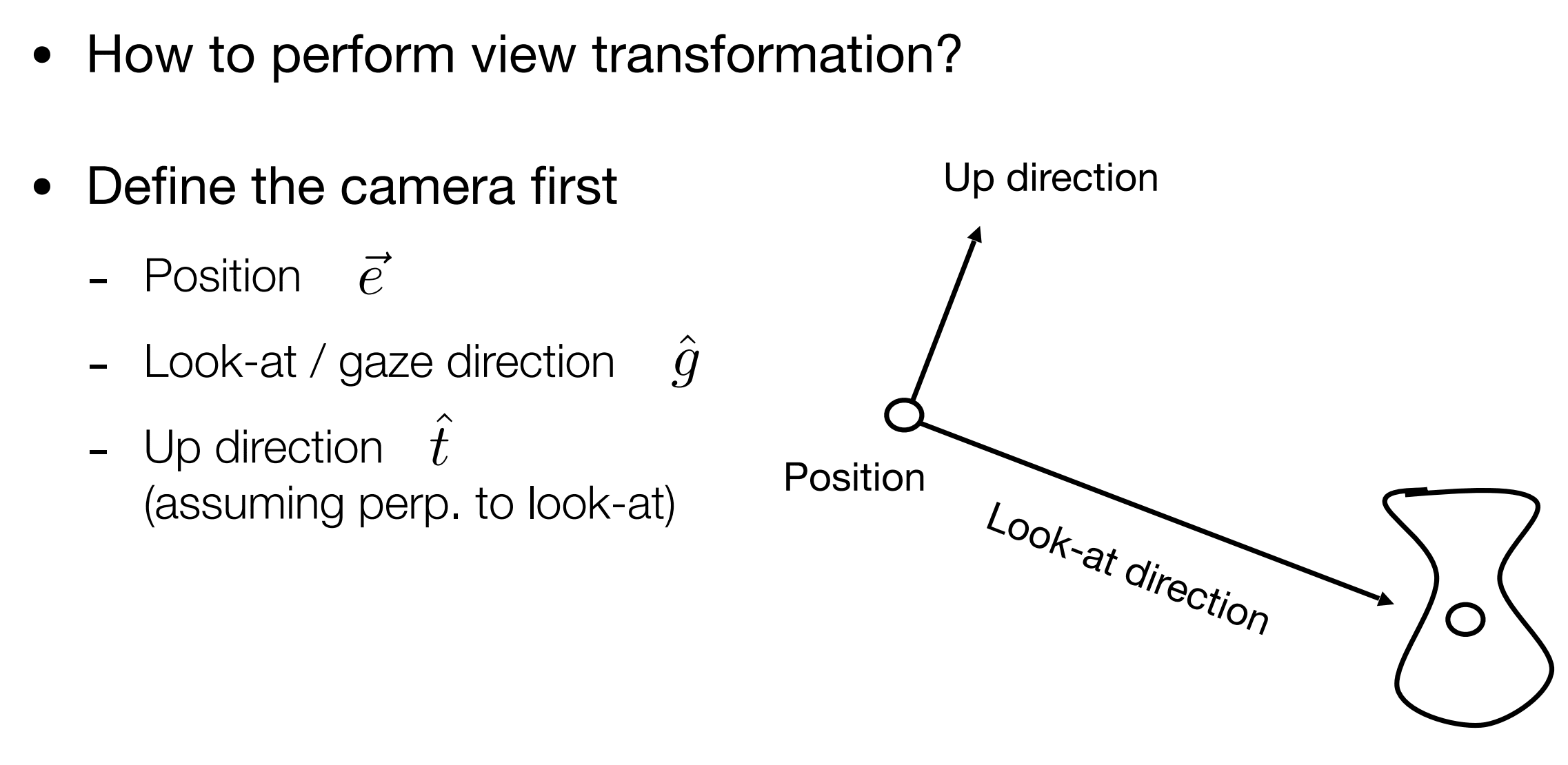
定义一个相机需要三个变量,位置,朝向,和一个向上的方向。
视图变换
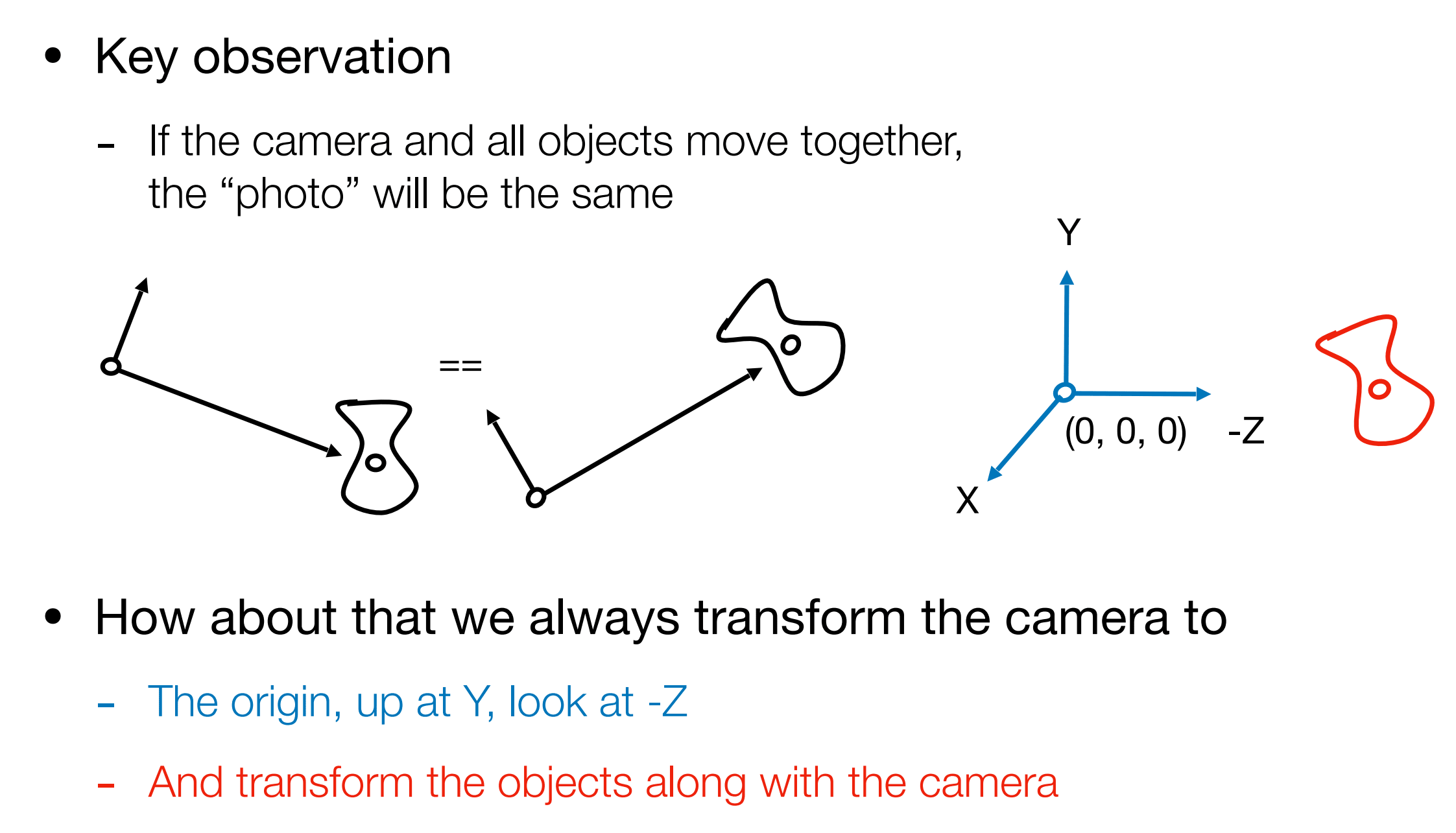
当相机和要拍的东西一起移动的时候,那拍出来的相片是一样的。也就是说,当我们移动物体时,只要同时以相同的方式移动相机,没有相对位置,那么得出来的结果就是一样的。
如果我们将相机放在一个固定的位置上,那么所有东西在移动时,都可以认为是其他东西在移动,而相机一直在原点不动。相机永远往 -z 方向看,以 y 轴为向上方向(右手坐标系,符合 OpenGL 传统)。这是约定俗成的。相机放在原点有很多好处,能简化计算。
从坐标空间的角度来看,就是将物体和相机从世界空间转到观察空间(摄像机空间)。
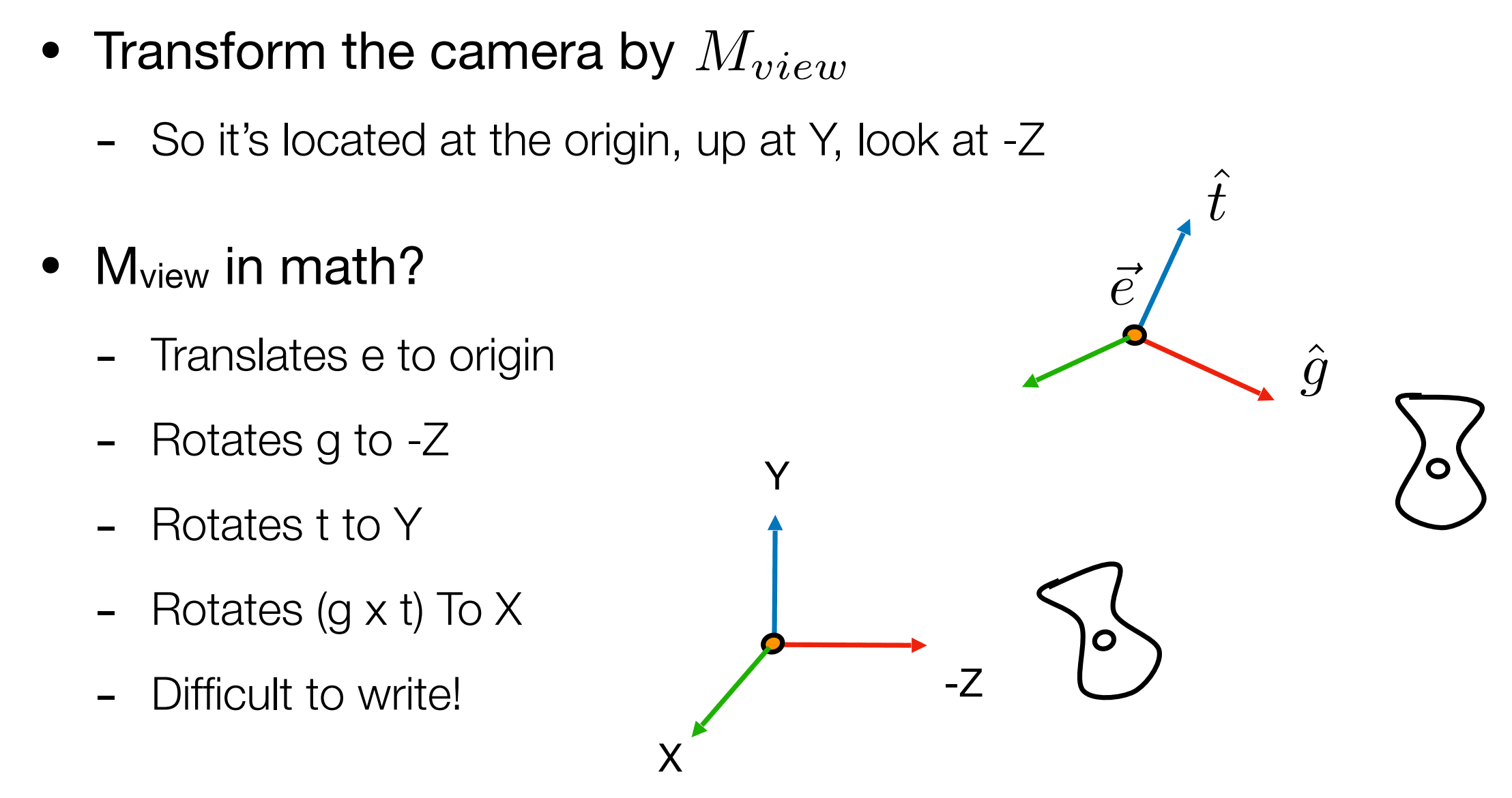
我们要将相机移到原点,就需要先把相机中心 e 平移到原点,还得把观察的方向 g 移到 -z 上,再把向上方向 t 旋转到 y 方向上,把 g X t 的方向移到 x 方向上。
下面将这系列操作转为矩阵操作。
求视图变换矩阵
- 先把相机中心 e 平移到原点
平移矩阵写好后,接下来写旋转矩阵。
- 把观察的方向 g 旋转到 -z 上,把向上方向 t 旋转到 y 方向上,g X t (g 叉乘 t)的方向旋转到 x 方向上
- Rotate g to -z , t to y, g X t To x (世界空间到观察空间)
- Consider its inverse rotation: x to g X t , y to t, z to -g (观察空间到世界空间)
我们可以反过来写,例如把 x 轴 (1,0,0 ) 旋转到 g X t 方向上的旋转矩阵,就比 g X t 移到 x 轴的旋转矩阵要好写很多,而这两个旋转矩阵是互逆的。写出 x 轴旋转到 g X t 方向的旋转矩阵后,再求其逆变换就是我们所需要的 g X t 移到 x 轴的旋转矩阵。
x to g X t , y to t, z to -g 的旋转矩阵就是:
这里 z to -g 是因为我们定义相机的坐标空间为右手坐标系。
要验证也很简单,用该旋转矩阵变换 x 轴就能得到 g X t 的方向。

那么我们的旋转矩阵就能通过对上面的矩阵求逆得出:
因为旋转矩阵是正交矩阵,因此要求逆矩阵,对其转置即可。
这样我们世界空间到观察空间的变换矩阵就能得出来了:M_view=R_view·T_view

其中 V_g×t 为 g×t 的向量,V_e 为相机原点。
相机需要进行这种变换,变换到约定俗成的位置(原点)上去,那么其他所有物体也需要做这样的变换,这样相对运动不变。这个就是视图变换。
模型变换和视图变换经常一起被称为模型视图变换(ModelView Transformation)。
Projection Transformation 投影变换
Projection in Computer Graphics
- 3D to 2D
- Orthographic projection
- Perspective projection
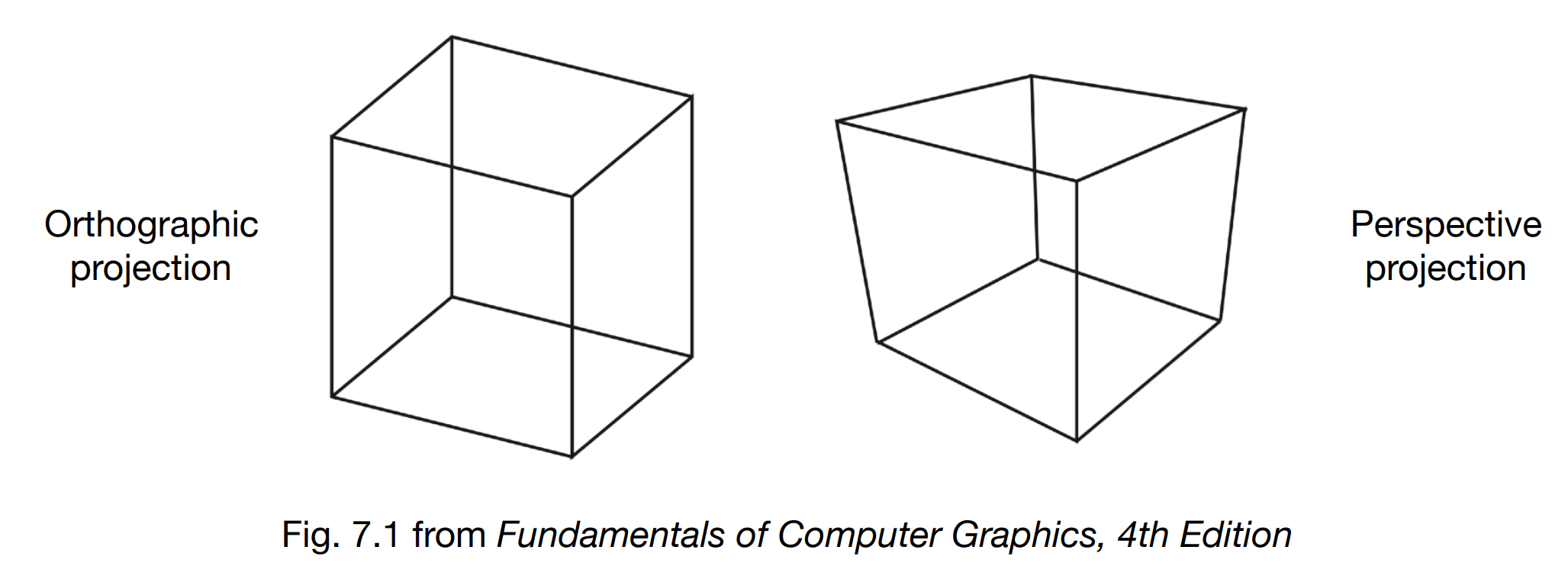
Perspective projection vs. orthographic projection
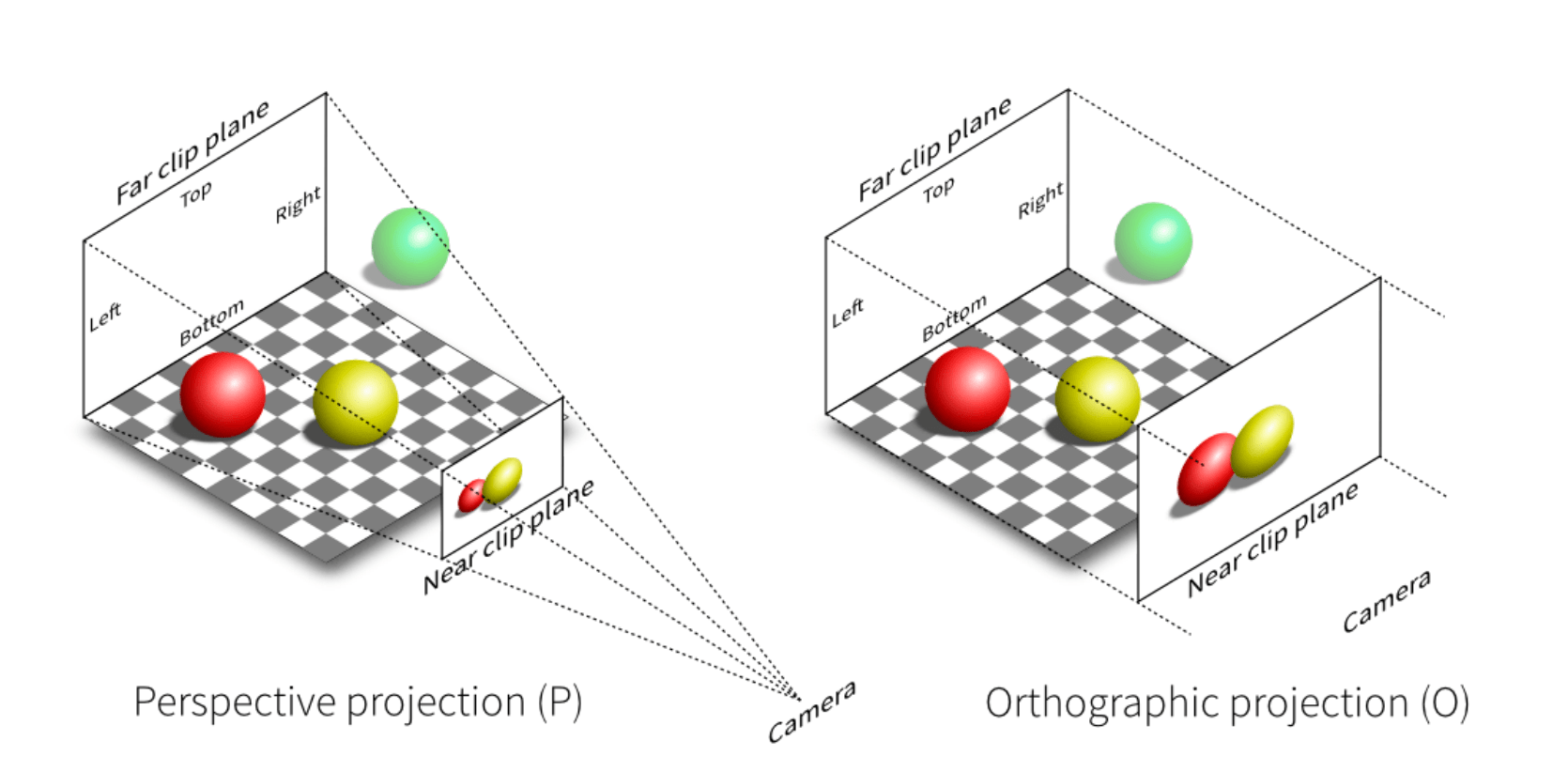
Orthographic Projection 正交投影
方法一
A simple way of understanding
- Camera located at origin, looking at -Z, up at Y (looks familiar?)
- Drop Z coordinate
- Translate and scale the resulting rectangle to
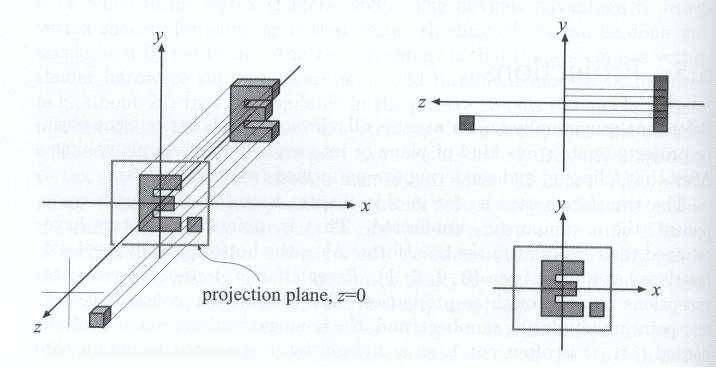
将坐标中的 z 扔掉,如何区分物体的前和后?
感兴趣可以参考 Catlikecoding Render 1 中 Orthographic Camera 部分。
方法二
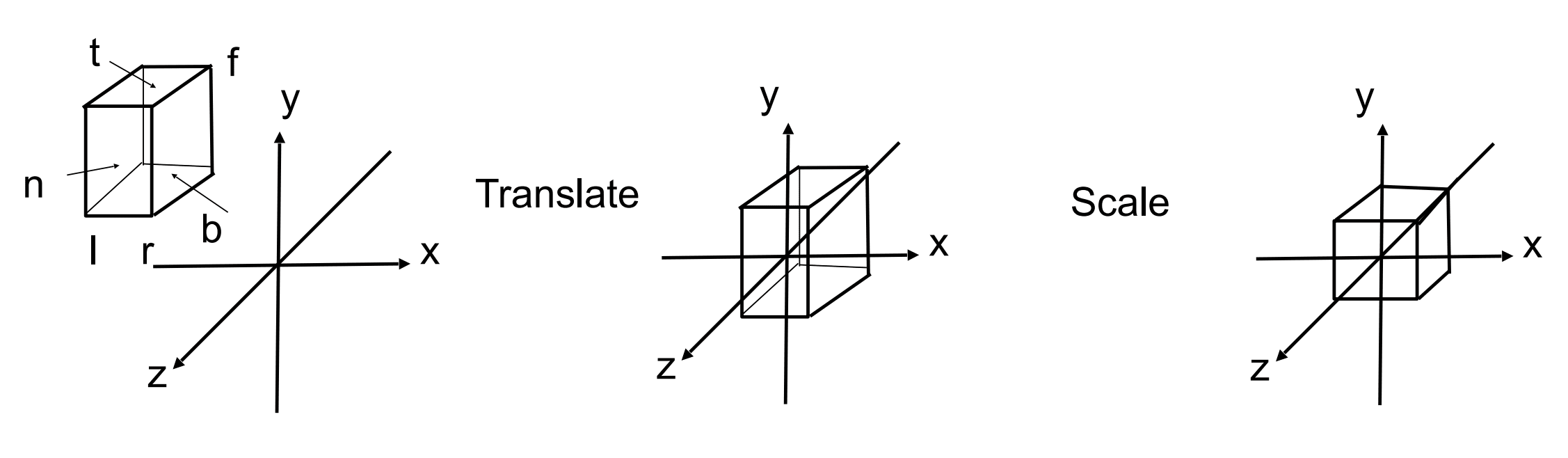
In general, we want to map a cuboid [l, r] x [b, t] x [f, n] to the “canonical (正则、规范、标准)” cube [-1,1]^3
我们在 x 轴上定义左和右 [l, r] (左比右小),y 轴上定义下和上 [b, t](下比上小),z 轴上定义远和近 [f, n](远比近小)。
不管 x, y 多大,都将其映射到 [-1, 1] 之间。这也是个约定俗成的事情,能方便计算。这样任何空间中的长方体,都可以映射成一个标准的立方体。
这也是**标准化设备坐标(NDC)**的定义。
上面的左比右小是相对于 x 轴来说的,下比上小是相对于 y 轴说的,但 z 轴上不太直观,因为我们推导的 NDC 是右手坐标系,(相机)看的是 -z 方向,因此一个面离我们远,说明 z 值更小。离我们近,说明 z 值更大。
在标准化设备坐标系中 OpenGL 使用的是左手坐标系,因为左手系在这一点上会比较方便。但也会造成别的问题:x × y ≠ z。
这里可以参考:LearnOpenGL 进入3D 的 右手坐标系 部分。
Slightly different orders (to the “simple way”)
- Center cuboid by translating 移到原点
- Scale into “canonical” cube 映射到 [-1, 1],也就是缩放
Translate (center to origin) first, then scale (length/width/height to 2) 因为 -1 到 1 的长度就是 2。
因此我们可以用一个平移矩阵和缩放矩阵来求出正交投影矩阵,先平移,再缩放:

如果把长方体范围缩成立方体,物体不会被拉伸吗?
会,这就涉及到另外一个变换。在所有变换做完之后,还要做一个视口变换,还要做一次拉伸。
Perspective Projection 透视投影
- Most common in Computer Graphics, art, visual system
- Further objects are smaller
- Parallel lines not parallel; converge to single point
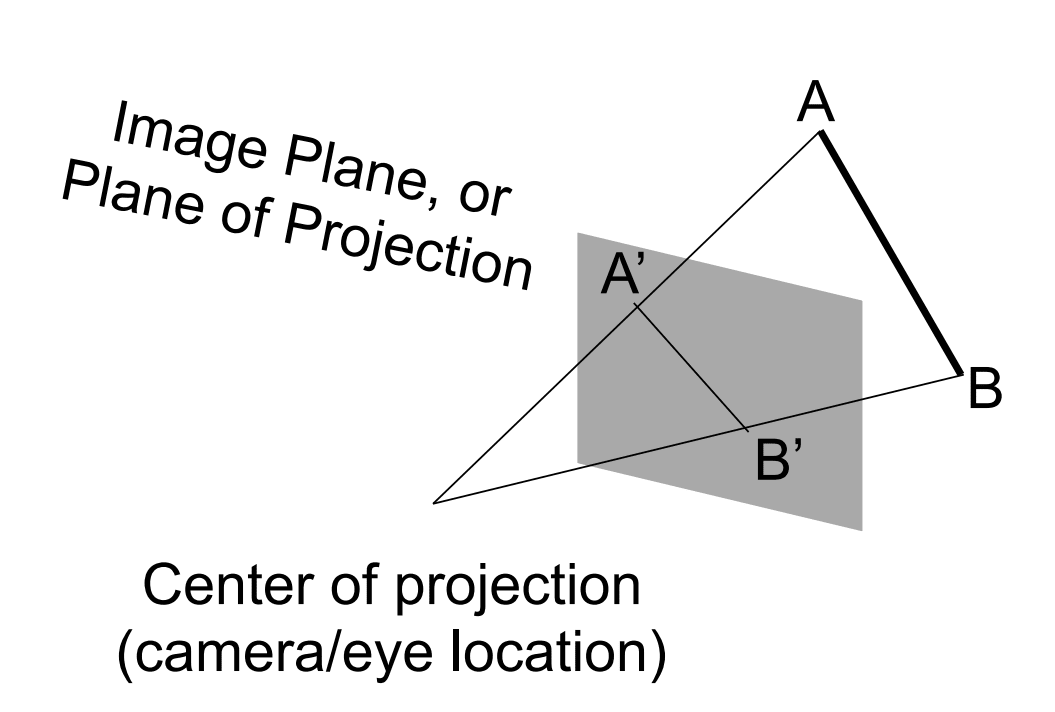

平行线就是永不相交的两条线,但照片上铁轨是平行的,却交于一点。透视投影的情况下,一个平面相当于被投影到了另外一个平面上,这种情况下就不是平行线了。
Recall
- Before we move on
- Recall: property of homogeneous coordinates
- (x, y, z, 1),(k x, k y, k z, k !=0), (x z, y z, z^2, z !=0) all represent the same point (x, y, z) in 3D
- 只要一个点乘于一个不为零的 k,那么它们还是一个点。那么我们还可以将其乘以 z,其表示的点还是空间中同样的点。下面我们会用到。
- e.g. (1, 0, 0, 1) and (2, 0, 0, 2) both represent (1, 0, 0)
- (x, y, z, 1),(k x, k y, k z, k !=0), (x z, y z, z^2, z !=0) all represent the same point (x, y, z) in 3D
- Simple, but useful
怎么做透视投影
How to do perspective projection
- First “squish” the frustum into a cuboid (n→n, f→f) (M_persp→ortho)
- Do orthographic projection ( M_ortho, already known!)
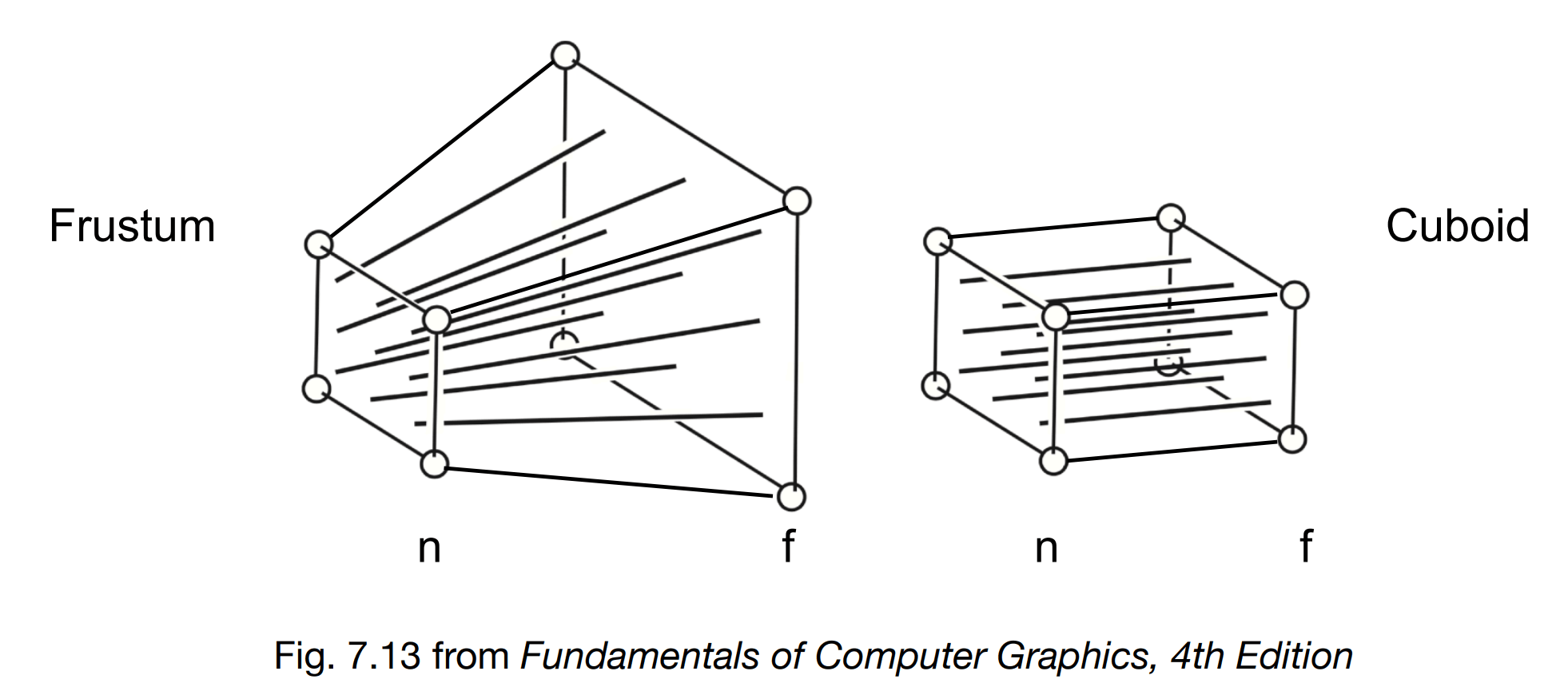
透视投影的视锥体中,远的平面比近的平面要大。
我们可以把远的平面往里“挤”,“挤”到同一高度且同近平面大小,“挤”成空间中的长方体,再做正交投影就解决了。
我们已经知道正交投影怎么做了,因此剩下的就是“挤”这个操作。
在这个过程中,需要规定:
- 近平面上任何一个点不变。
- Z 值不变
- 远平面的中心也不会发生变化
求出任何一个点挤压后的 x’, y’ 值
要做“挤”的操作,首先要知道任何一个点的 x, y 值是怎么变化的。因为我们任何一个面都要挤成近平面大小,我们也可以将 (x,y,z) 投影到近平面上求出变换后的 x’, y’ 值。对于 x, y 值来说,这种变换是线性的。
因此,在视锥体的上面一部分中,我们可以通过相似三角形求出变换后的 x’, y’ 值。(z’ 值不是线性变化的,后面会提到)
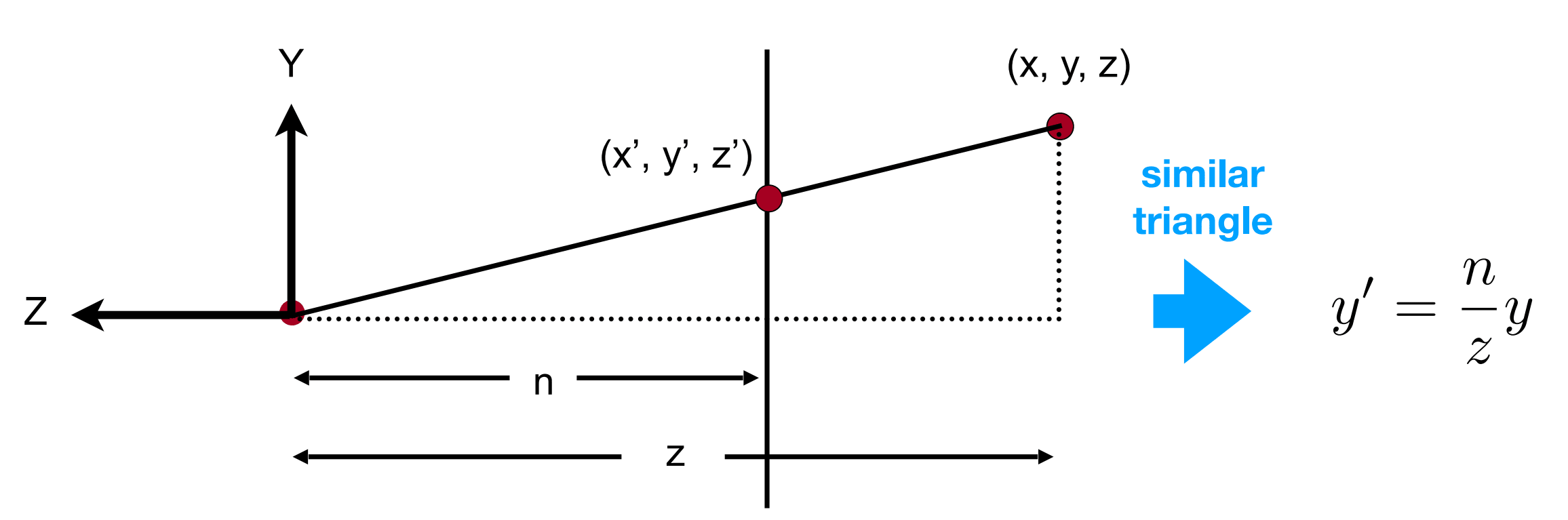
上图中,n 为近平面的 z 值,z 为任何一个点(x,y,z)中的 z 值。
挤压后的 y’ 值,我们可以通过相似三角形原理得出:
同理可得挤压后的 x’ 值:
在齐次坐标系中,对于变换后的 (x’, y’, z’) 我们只剩下 z’ 未知。
这里给矩阵乘了 z,其表示的点还是空间中同样的点。

也就是说 (x,y,z,1) 经过 Mpersp→ortho 矩阵“挤压”后,会被映射到 (nx,ny,??,z):
根据上式,我们可以得出部分的 Mpersp→ortho 矩阵:
对于 z,我们不知道 z 会怎么变,我们只规定了近的平面上和远的平面上 z 不变。
Observation: the third row is responsible for z’
- Any point on the near plane will not change
- 近平面的点不变,对于任何 (x,y,n,1) 运算完了一定还是 (x,y,n,1)
- Any point’s z on the far plane will not change
- 远平面的点,虽然 x, y 会变化,但是 z 没有变。
求出任何一个点挤压后的 z’ 值
由“近平面的点不变,对于任何 (x,y,n,1) 运算完了一定还是 (x,y,n,1)”可得:
这里给矩阵乘了 n,其表示的点还是空间中同样的点。

因此 Mpersp→ortho 第三行一定是 (0,0,A,B) 的形式,因为:

由上式可得:
前面我们已经知道第三行前两个数是 0。
我们前面已经规定了远平面的中心经过 Mpersp→ortho 变换后也不会发生变化。
另外一个等式可以用远平面可以用其特殊的中心点得出,给中心点再乘个 f 可得:

平截头体(Frustum)被压缩成长方体以后,内部的点的 z 值是更偏向于近平面还是更偏向于远平面?
可以参考 ScratchAPixel 的 The Perspective and Orthographic Projection Matrix
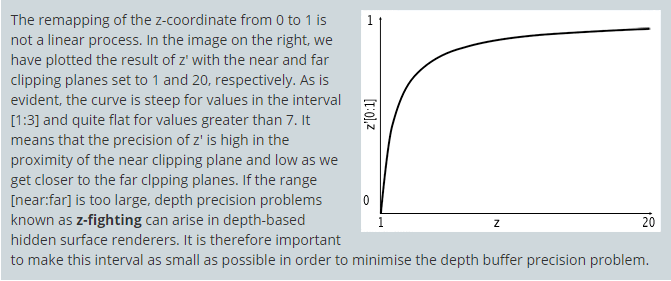
定义视锥
前面提到了长方体近平面的 l, r, b, t,有没有更好的方法去定义这些呢?
vertical field-of-view (fovY) and aspect ratio
我们现实中相机有视角的定义,也就是可以看到的角度的范围,也就是 field of view。广角相机就是可视角度比较大,对于视锥体来说,就是张的比较开。
垂直的可视角度就是 fovY。而相机的长宽比就是 aspect ratio。
我们也可以通过 fovY 和 aspect ratio,来推出水平的可视角度。
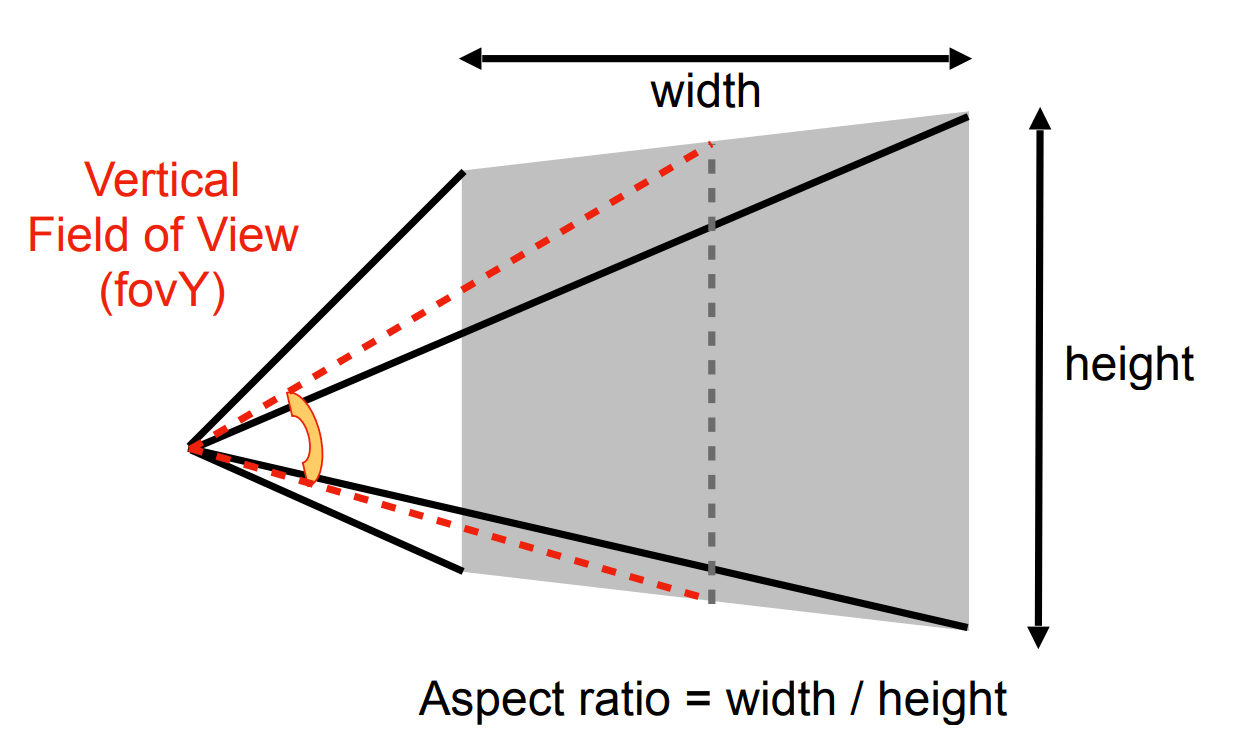
How to convert from fovY and aspect to l, r, b, t?
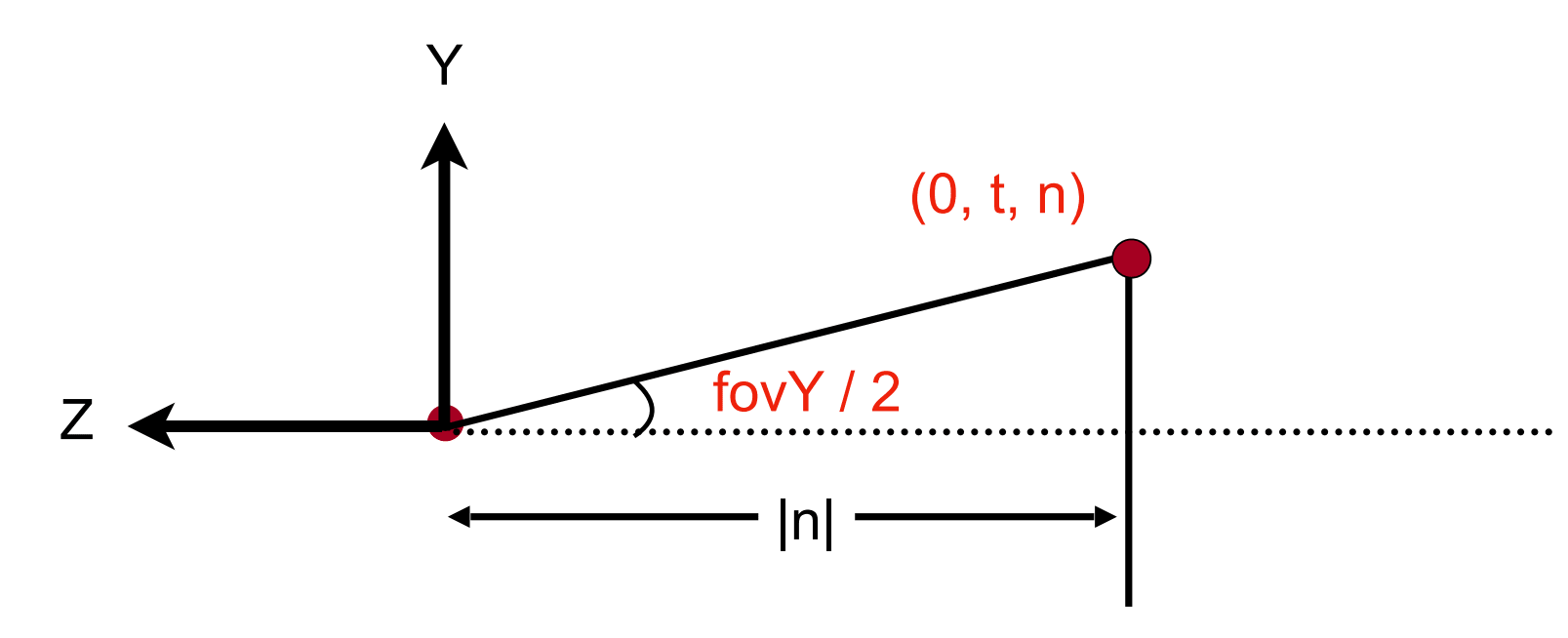

完成推导正交投影矩阵
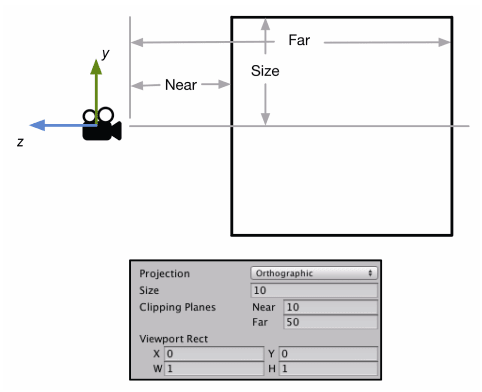
正交投影没有 fovY,在 Unity 中,正交投影的参数由 Camera 组件中的参数 Size, Near, Far(Viewport Rect 暂时忽略)和 Game 视图的横纵比(aspect ratio)共同决定。
这里的 Near 是近裁面的距离,也就是 -n,Far 同理,等于 -f。
Size 属性用来更改视锥体竖直方向上高度的一半,也就是前面近平面的高度 t。
由此可得正交投影近远平面的高度 t-b 为:2·Size=2·t
正交投影近远平面的宽度 r-l 为:
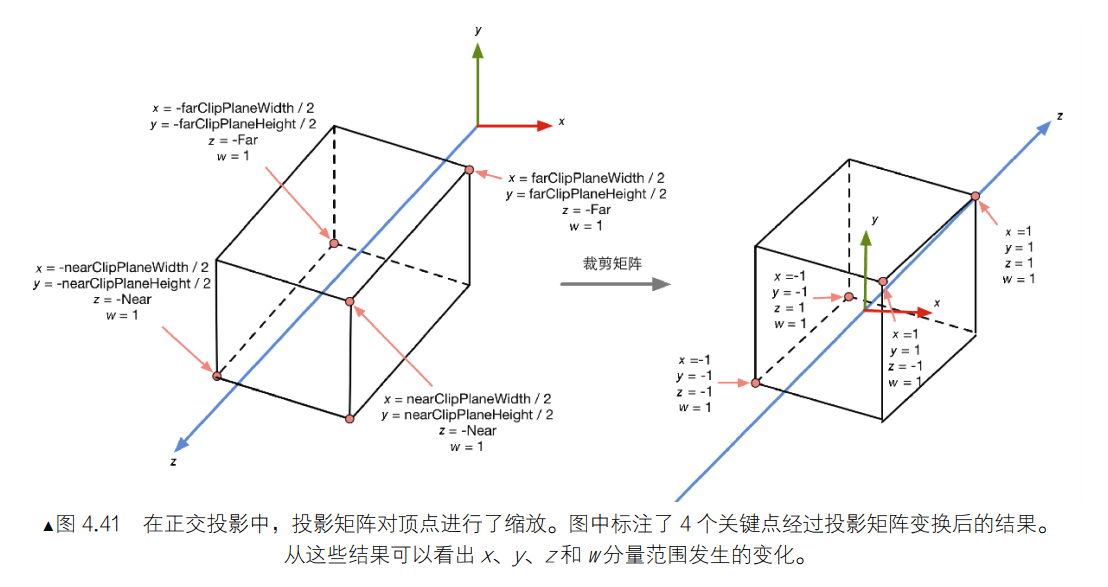
注意:这里的 n 和 f 是 -z 轴上的,代表近裁面和远裁面的 z 值,值为负数。
完成推导透视投影矩阵
前面已经得出:


注意:这里的 n 和 f 是 -z 轴上的,代表近裁面和远裁面的 z 值,值为负数。
通常我们透视投影的参数除了近裁面远裁面的距离外,还会有 fov 和 Aspect,且 r+l=0,因此整理公式可得:

后记
在长文的最后,我强烈推荐大家也手推一下各种变换,n, f 取 -z 轴上的 z 值或绝对值(也就是距离)得出来的变换矩阵也不一样,都推导一遍可以理解更深刻。
此外,我们也可以开始实现一个简单的 CPU 软光栅渲染器,我近期也在准备写一个软光栅,把必要的过程都推导一遍,到时候再写博文分享一下。









