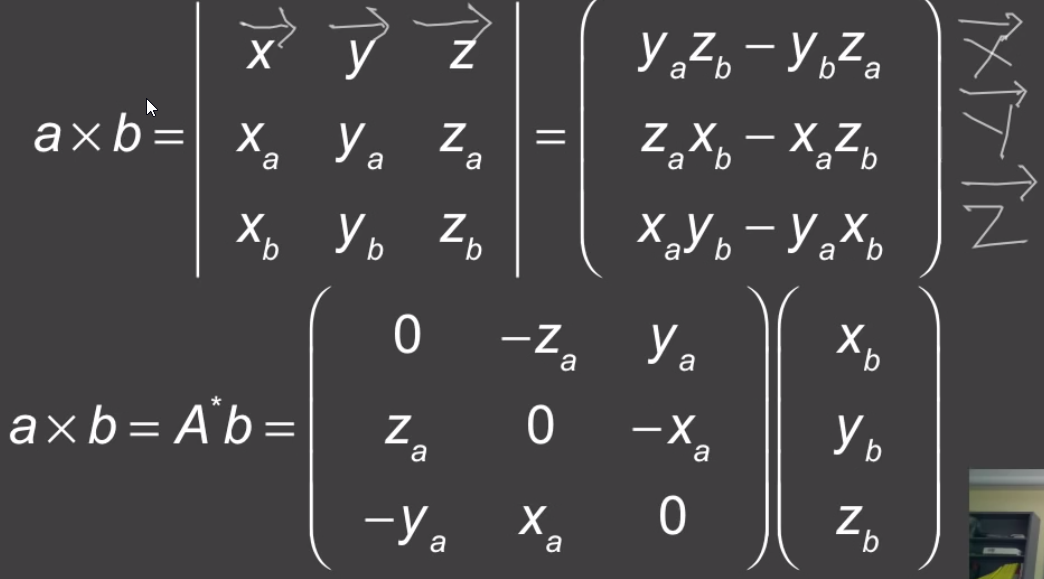2020年7月26日更新:
最近对变换重新学习整理了,文章在:图形学常见的变换推导。
最近在跟公开课 edx 的 Computer Graphics(想一起学的告诉我!),这篇笔记主要介绍了图形学中会用到的比较基础的3D数学,重拾大学线性代数知识。
基础运算
点积(Dot Product)
将向量相乘得到一个标量
可以通过两个向量除以它们的模得到两个向量之间的夹角
用途:
- 求两个向量之间的夹角(光源和表面之间夹角的余弦值对于投影来说非常重要)
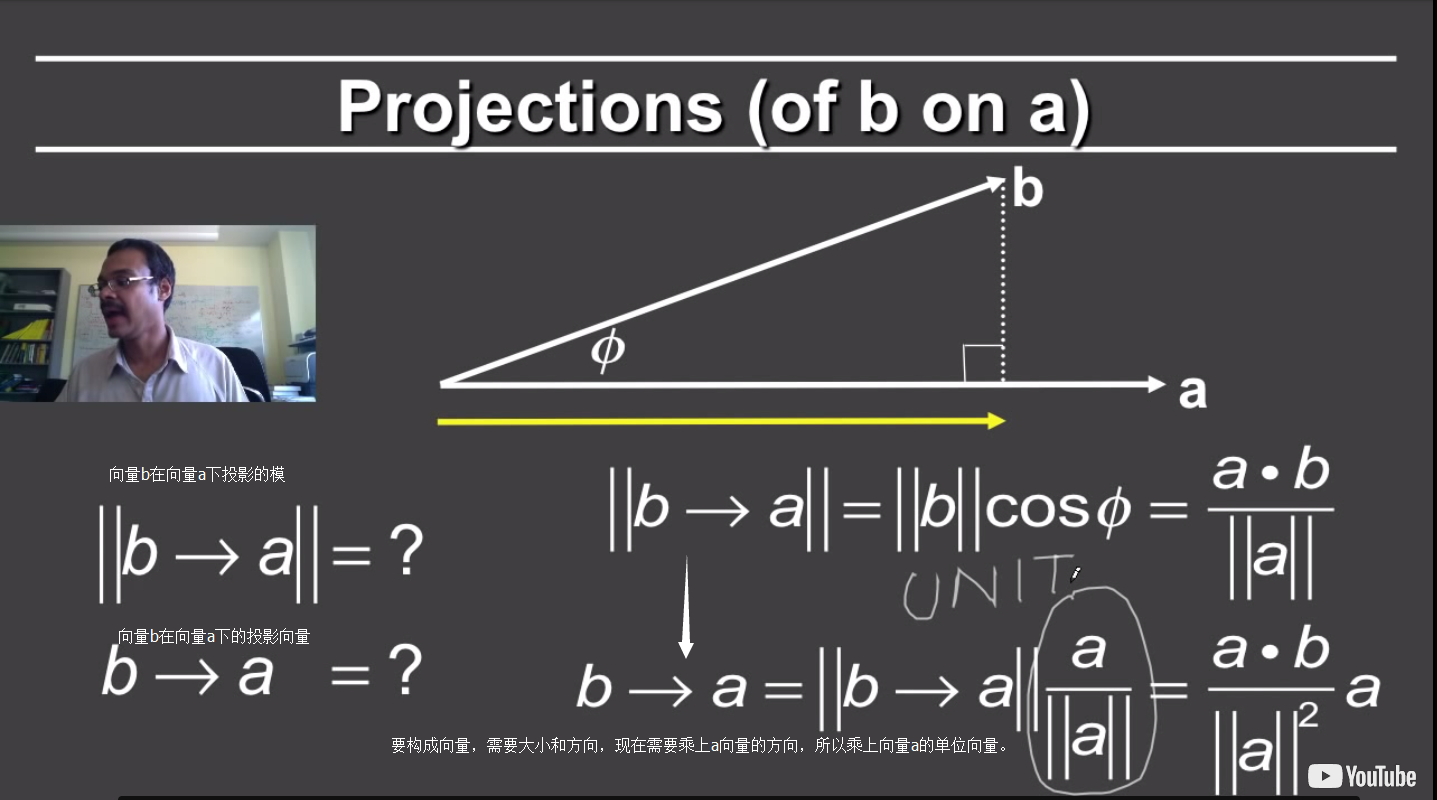
- 找到一个向量在另一向量上的投影也非常重要(比如我们想知道一个点在新的坐标系下的坐标)。
- 点积在笛卡尔坐标系下很有用
a⋅b=∥a∥∥b∥cosθ
叉积(Cross Product)
将向量相乘得到一个正交向量(垂直于向量a和向量b)
a×b=−b×a∥a×b∥=∥a∥∥b∥sinθ
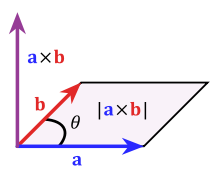
叉积所得到的向量的方向可以通过右手坐标系来得到:
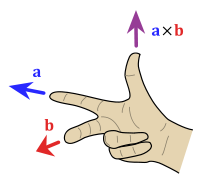
用右手食指代表叉积中前一个向量,用中指代表叉积中后一个向量,则大拇指的方向就是叉积得到的向量方向。这简单的方法能提醒你:将进行叉积的两个向量顺序调换的话,得到的向量方向会相反。

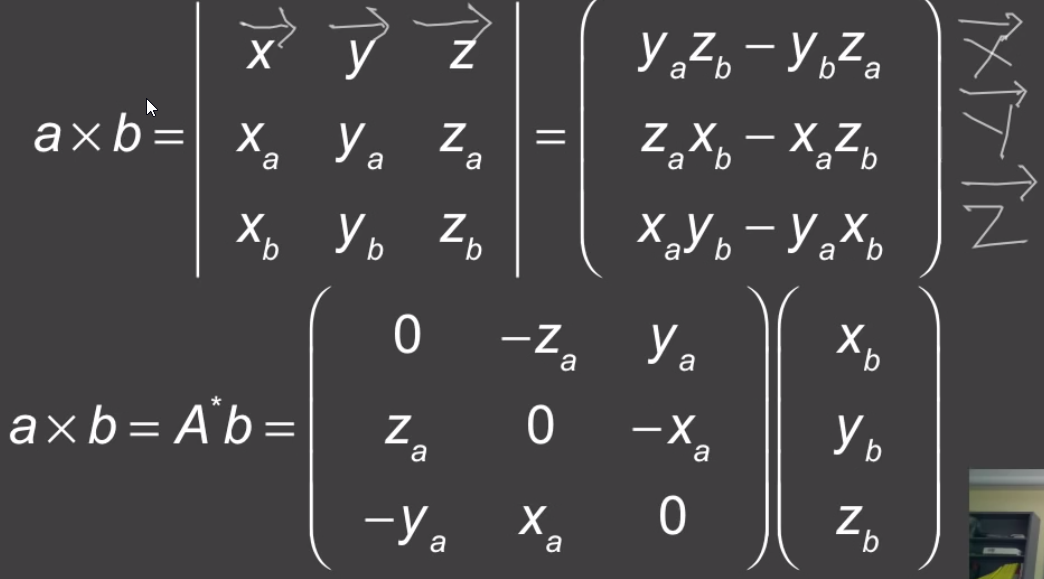
叉积可以用向量 a 的对偶矩阵来完成,所以可以将它表示成A星(A*)乘以b,其中A*是向量a的对偶矩阵(共轭转置)。
正交坐标系
正交基和坐标系对于表示点的位置非常重要,因为在图形学中,我们通常需要很多不同的坐标系,来表示点在不同参照物下的位置。例如:要表示自己身前一台电脑的位置,可以在自己的位置建立一个坐标系来表示电脑的位置;要表示北极的位置时,用地球的坐标系表示北极的位置会更容易。


矩阵
图形学中矩阵很重要,因为大多数变换都涉及一个矩阵乘以一个向量,矩阵可以用来变换点。下面简单的列一下矩阵的性质,更多的性质可以参考下维基页面矩阵。
矩阵相乘

矩阵相乘时,乘积处(i,j)处的元素是:第一个矩阵的 i 行和第二个矩阵 j 列的点积,这也是为什么要求第一个矩阵的列数等于第二个矩阵的行数。
矩阵转置
147102581136912T=123456789101112
adgbehcfiT=abcdefghi
[xyz]T=xyzxyzT=[xyz]
(AB)T=BTAT
矩阵的逆
(MT)−1=(M−1)T
(M1M2⋯Mn−1Mn)−1=Mn−1Mn−1−1⋯M2−1M1−1
M−1=1/∣M∣
矩阵与矩阵的逆相乘得到单位矩阵:
M(M−1)=M−1M=I
矩阵变换
缩放
二维空间下和三维空间下的缩放很简单,直接乘上相应的缩放倍数即可。


切变
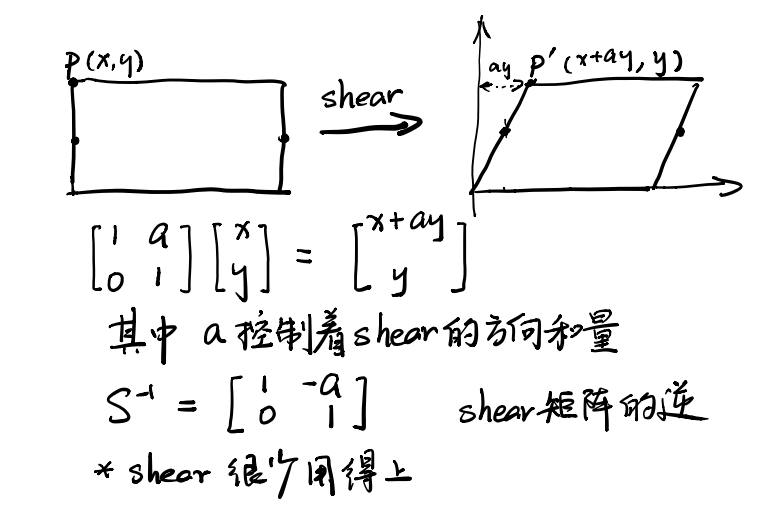
旋转
二维空间下的旋转
二维空间下,物体的旋转可以靠矩阵在X方向的变换于矩阵在Y方向的变换叠加得到,但不适用于三维空间。
下面是推导过程:
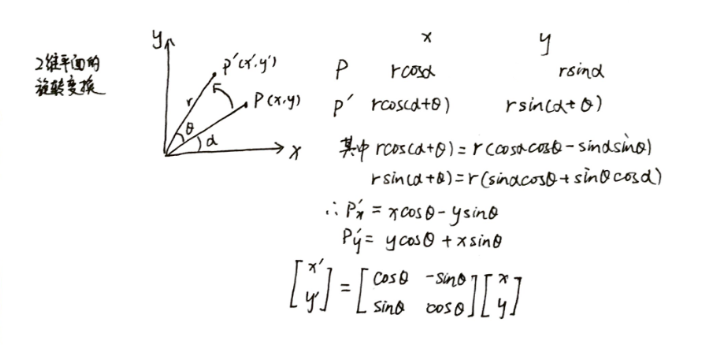

这三种矩阵变换不符合交换律,也就是说变换的顺序改变会得到不同的结果,要恢复变换的话也要从最后一次变换开始恢复。(Unity 的默认变换顺序是先缩放,再旋转,最后平移)

三维空间下的旋转
下图分别给出了绕 Z 轴旋转、X 轴旋转和 Y 轴旋转的变换矩阵:

二维旋转可以看作是绕着 Z 轴的特殊旋转,因为 Z 轴保持不变。因此 Rz(绕着 Z 轴的旋转)可以直接在二维空间旋转矩阵外的 Z 轴处填充 1 和 0 来使用,同理可得绕X轴的旋转矩阵和 Y 轴的旋转矩阵。
绕任意轴旋转

在这其中,三个正交向量(相互垂直)可以构成一个旋转矩阵,这样就可以将点映射到新的坐标系下。这个概念非常重要,因为在图形学中常常需要这样的变换,如把每个3D模型的顶点的法线从模型空间转到剪裁空间(不同的坐标系)再统一进行计算。
这个旋转矩阵的逆只需要将 XYZ 轴换成 u,v,w 即可。

详见罗德里格旋转公式
下一篇笔记会写更多关于三维空间下的矩阵变换。
参考资料